ТЕСТЫ
для промежуточного и итогового контроля знаний
1.
Матрица,
у которой число строк равно числу столбцов называется:
а) диагональной; б)
прямоугольной; в) квадратной; в) нулевой.
2.
Вычислите определители второго порядка:
1) ![]() ; а) 8;
; а) 8;
2) ![]() ; б)
-3;
; б)
-3;
3) ![]() ; в)
0;
; в)
0;
4) ![]() ; г)
12.
; г)
12.
3.Определитель
равен:
1)
![]() ; а)
-
; а)
-![]() ;
;
2)
![]() ; б)
-2;
; б)
-2;
3)
![]() ; в)
; в)
![]() -
-![]() ;
;
4)
![]() ; г)
; г)
![]()
- Найти корни уравнения:
![]() =
= ![]() ;
;
Ответы: а) 1; б)
-![]() ; в) 3; г) -3.
; в) 3; г) -3.
5. Вычислить
алгебраические дополнения определителя:

1)
А11;
2) А22; 3) А23;
4)А31:
Ответ: а)0; б)-5; в) -3; г) 3; д) -2; е)-6.
6. Найти корни уравнений:
1)  = 0; а)
2;
= 0; а)
2;
2) 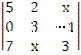 = -1; б) -6;
-4;
= -1; б) -6;
-4;
3) 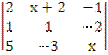 = 0; в) -1; 0; 1.
= 0; в) -1; 0; 1.
7. Дана система уравнений:

Выберите правильное утверждение:
1) система определенная; 2) система несовместная; 3)
система неопределенная.
8.
Установить соответствие между СЛУ и решениями:
1) ![]() а) (2; 3);
а) (2; 3);
2)![]() б)
несовместна;
б)
несовместна;
3) ![]() в) (3;
3).
в) (3;
3).
9. Вычислить определители третьего порядка:
1) 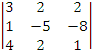 ; а)
0;
; а)
0;
2) 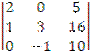 ; б)
11;
; б)
11;
3) 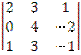 ; в)
87;
; в)
87;
4)  ; г)
-6.
; г)
-6.
10. Для какой из систем (1; 1; 1 ) являются решением?
а) 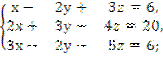 б)
б) 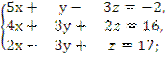
в)  г)
г) 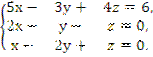
11.
Установить соответствие между рисунками и векторными равенствами:

а) ![]() +
+![]() +
+![]() =
=![]() б)
б) ![]() +
+![]() =
=![]() в)
в) ![]() -
-![]() +
+![]() =
=![]() г)
г) ![]() -
-![]() =
=![]()
12. Заданы пары
векторов:
1) ![]() (3; -3; 3),
(3; -3; 3), ![]() (-1; 1;- 1); 2)
(-1; 1;- 1); 2) ![]() (-1; 2; -2),
(-1; 2; -2), ![]() (2; -4; 4); 3)
(2; -4; 4); 3) ![]() (4; -4; -2),
(4; -4; -2), ![]() (1; -1; -0,5);
(1; -1; -0,5);
4) ![]() (3; 1),
(3; 1), ![]() (-4; 12); 5)
(-4; 12); 5) ![]() (1; -2; 3),
(1; -2; 3), ![]() (-2; 4; -6).
(-2; 4; -6).
Назовите пары: а) коллинеарных векторов; б)
перпендикулярных векторов.
13. Векторы: а) коллинеарные; б) перпендикулярные;
в) имеют равные длины:
1) ![]() (1; -2; 6) и
(1; -2; 6) и ![]() (-1; 6; 2);
(-1; 6; 2);
2) ![]() (-5; 2; 3) и
(-5; 2; 3) и ![]() (10; -4; -6);
(10; -4; -6);
3) ![]() (-3; 2; 1) и
(-3; 2; 1) и ![]() (4; 6; 0).
(4; 6; 0).
14. При каком значении k векторы являются
коллинеарными:
1. ![]() (1;-1;1) и
(1;-1;1) и ![]() (k;3;-3); а)
-24;
(k;3;-3); а)
-24;
2. ![]() (4;6;k) и
(4;6;k) и ![]() (
(![]() ;-
;- ![]() ;3); б)
-1;
;3); б)
-1;
3. ![]() (-2k; 2k+2; -2)
и
(-2k; 2k+2; -2)
и ![]() (3;-4; 1); в)
-3;
(3;-4; 1); в)
-3;
4. ![]() (2k; 3; 4) и
(2k; 3; 4) и ![]() (4;-6; -8); г)
3.
(4;-6; -8); г)
3.
15. Чему равно скалярное произведение векторов ![]() если:
если:
1) ![]() и
и![]() коллинеарные и одинаково направленные; а)
х2+у2+z2;
коллинеарные и одинаково направленные; а)
х2+у2+z2;
2) ![]() и
и![]() противоположные; б) х1х2+у1у2+z1z2;
противоположные; б) х1х2+у1у2+z1z2;
3) ![]() и
и![]() в)
-х2-у2-z2;
в)
-х2-у2-z2;
4) ![]() и
и![]() равные? г)
0.
равные? г)
0.
16. Найдите соответствие между заданными прямыми и
видами этих прямых:
1) Ах + Ву + С = 0; а)
уравнение прямой в общем виде;
2) ![]() +
+ ![]() = 1; б)
уравнение прямой, заданной 2мя точками;
= 1; б)
уравнение прямой, заданной 2мя точками;
3) ![]() =
= ![]() ; в)
уравнение в отрезках;
; в)
уравнение в отрезках;
4) А∙(х - х0)+ В∙(у – у0) + С
= 0; г) уравнение прямой, заданной с
помощью точки
и
направляющего вектора;
5) ![]() =
= ![]() ; д)
уравнение пучка прямых;
; д)
уравнение пучка прямых;
6) у – у0 = k ∙(х – х0); е)
уравнение прямой, заданной с помощью точки
и
перпендикулярного вектора;
17. Какие из
заданных прямых перпендикулярны прямой 2х – у + 3 = 0;
1) 4х +8у + 17 = 0; 2) 4х -8у – 11 = 0; 3) у = - ![]() 4) у = -2х – 7; 5)
4) у = -2х – 7; 5) ![]()
18. Найдите соответствие между заданными уравнениями
и видами кривых второго порядка:
1) 3х2 – 4у2 = 12 ; а) уравнение эллипса;
2) х2 + у2 + 10х – 4у – 20 =
0; б) уравнение параболы;
3) 5х2 + 4у2 = 20; в)
уравнение окружности;
4) х2 = 8у; г)
уравнение гиперболы.
19. Привести
кривые второго порядка к каноническому виду и указать вид кривой:
1) х2
= ![]() а)
а)
![]() А)
уравнение окружности;
А)
уравнение окружности;
2) 5х2 – 3у2 = 75; б)
у = 8х2; Б)
уравнение параболы;
3) х2 + у2 – 4х + 6у – 23 = 0; в)
![]() В)
уравнение гиперболы;
В)
уравнение гиперболы;
4) 4х2 + 9у2 = 144; г)
(х-2)2+ (у+3)2 = 46; Г)
уравнение эллипса.
20. Проверить, какие векторы перпендикулярны:
1) ![]() =(-3; 2) и
=(-3; 2) и ![]() =(4; 6); 2)
=(4; 6); 2) ![]() =(
=(![]() ; -
; -![]() ) и
) и ![]() =(
=(![]() ; 5); 3)
; 5); 3) ![]() (-2; 5) и
(-2; 5) и ![]() =(3; 1).
=(3; 1).
21. Определите угол между векторами: ![]() =(-3; 2) и
=(-3; 2) и ![]() =(2; 3).
=(2; 3).
22. Выясните, какие из функций
являются ограниченными:
1) у = ![]() ; 2) у =
; 2) у = ![]() 3) у =
3) у = ![]() 4) у =
4) у = ![]()
23. Выясните, какие из функций являются монотонными
при хє (![]()
1) у = х2; 2)
у = х3; 3) у = ![]() 4)
у =
4)
у = ![]()
24. Выясните,
какие из функций являются нечетными:
1) у = ![]() +
+![]() 2) у =
2) у =![]() 3)
у = х3 +
3)
у = х3 + ![]() 4)
у =
4)
у = ![]() 3
3![]()
25.
Укажите верные утверждения для функции у
= ![]()
1) монотонная; 2) ограниченная; 3) неограниченная; )
четная; 5)
нечетная;
6) общего вида; 7) явно
задана; 8) неявная; 9) сложная.
26. Выясните, какие
из перечисленных функций бесконечно
малые при х→0:
1) у = ![]() ; 2)
у =
; 2)
у = ![]() 3)
у =
3)
у = ![]() 4)
у =
4)
у = ![]() 5)
у =
5)
у = ![]() .
.
27. Выясните, какие из
перечисленных функций бесконечно большие при х→![]()
1) у = ![]() 2) у =
2) у = ![]() 3)
у =
3)
у = ![]() 4)
у =
4)
у = ![]() 5)
у =
5)
у = ![]()
28. Выясните, какие из перечисленных функций непрерывны в точке х =
0:
1) у = ![]() ; 2)
у =
; 2)
у = ![]() 3)
у =
3)
у = ![]() 4)
у =
4)
у = 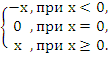
5) у = ![]()
29. Выясните, какие из
функций являются непрерывными, но не дифференцируемы
в точке х0:
1)
у = |х+2|, х0=2; 2)
у = |х-5|, х0=5; 3) у = ![]() х0=8; 4) у =
х0=8; 4) у = ![]() х0=π;
х0=π;
5) у = ![]() , х0=0.
, х0=0.
30. Выясните, какие из функций являются дифференцируемыми в точке х0=1:
1) у = ![]() ; 2)
у = х∙
; 2)
у = х∙![]() 3)
у =
3)
у = ![]() ;
;
4) у = х2∙![]() 5)
у = |3х-2|.
5)
у = |3х-2|.
31. Установить соответствие между графиками функций
у = f![]() (1, 2, 3) и графиками их производныху' = f
(1, 2, 3) и графиками их производныху' = f![]() (а, б. в):
(а, б. в):

32. Предложенные
формулы позволяют:
1) у' (х) = ![]() ; а) найти
дифференциал функции ;
; а) найти
дифференциал функции ;
2) dy = y'(x)dx; б)
дать понятие производной;
3) ![]() (x + ∆x) ≈
(x + ∆x) ≈ ![]() (x0)
+
(x0)
+ ![]() ´(x0)dx; в)
найти угол наклона касательной;
´(x0)dx; в)
найти угол наклона касательной;
4) y'(x0)
= tq![]() ; г)
составить уравнение касательной;
; г)
составить уравнение касательной;
5) у – у0 = y'(x0)∙(х-х0); д) найти
приближенное значение функции.
33. Составить уравнение
касательной к графику функции у = 4х – х2 в точке х0=3.
Ответ: у = кх+в, где к
= …; в = … .
34. Найдите область определения функции:
1) у =![]() ; а) (
; а) (![]() ; б) (1;+
; б) (1;+![]() в) (
в) (![]() г) (
г) (![]()
2) у = ![]() ; а) (-2; 1); б) [-1; 2]; в) (-2; -1); г)
[-2;1].
; а) (-2; 1); б) [-1; 2]; в) (-2; -1); г)
[-2;1].
3) у = ![]() ; а)
(-1; 1); б) (
; а)
(-1; 1); б) (![]() в) [-1; 1]; г) (-1; +
в) [-1; 1]; г) (-1; +![]() ).
).
35. Определите, содержат ли неопределенности ( если
да, то какого типа) следующие пределы:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() - х).
- х).
Ответ: а) ![]() б)
б) ![]()
36. Назовите некоторые методы раскрытия
неопределенностей типа: ![]() 2
2![]()
![]()
![]()
37. Найти пределы функций:
1) ![]() ; а) 2;
; а) 2;
2) ![]() ; б)
; б) ![]() ;
;
3) ![]() в) 1,5.
в) 1,5.
4) ![]() г)
г) ![]()
38. Среди перечисленных функций убывает на всей
области определения
функция:
1)
у = ![]() 2) у =
2) у = ![]() ; 3) у =
; 3) у = ![]() 4) у = х3 – х2; 5) у = х3
+ х2.
4) у = х3 – х2; 5) у = х3
+ х2.
39. Выяснить, какое из приведенных утверждений
является неверным:
1) в точке экстремума производная функции равна нулю или не существует;
2) в точке экстремума функция меняет знак;
3) в точке экстремума производная меняет знак;
4) в точке, в которой проиводная равна нулю или не
существует, может не быть экстремума?
40. Дописать формулы:
1) (U
![]() ′=
…; 2) (СU)′
= …; 3) (…)′ = -
′=
…; 2) (СU)′
= …; 3) (…)′ = - ![]() ;
4) (…)′ = U′V + … ;
;
4) (…)′ = U′V + … ;
5) ![]() )′
= n∙х…;
6) (f(U))′ = f′…∙U′… .
)′
= n∙х…;
6) (f(U))′ = f′…∙U′… .
41. Найти производные функций:
1) у = (![]() 3; а)
3; а) ![]() -
- ![]()
2) у =![]() +
+ ![]() ; б)
; б) ![]() ;
;
3) у = ![]() ; в)
; в)![]() +
+ ![]() ;
;
4) у = х∙![]() –
– ![]() ; г) 3(1 +
; г) 3(1 + ![]() )2
)2![]() .
.
42. По графику функции определить:
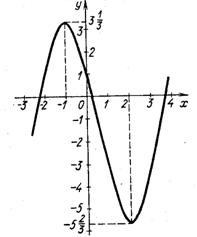
1) промежутки возрастания функции; а) (-1;2);
2) промежутки убывания функции; б) (-![]()
3) абсциссу точки максимума; в) 2;
4) абсциссу точки минимума; г) -1.
43. точка движется по закону:
1) S = 2t3+t2-4; 2) S = t3+t2+4t; 3) S =
3t2 -2t; 4) S = 2t3+t2+t.
Найти скорость движения точки в конце второй
секунды.
Ответ: а) 20 м∕с; б) 29 м∕с; в) 28 м∕с; г) 10 м∕с.
44. Найдите ускорение в момент времени t =3с для
точки, движущейся прямолинейно, если скорость задана уравнением:
1) V=t2+t-1;
2) V=t2+5t+1; 3) V=t2+2t-3; 4) V=t2+4t-2.
Ответ: а) 10; б) 8; в) 11; г) 7.
45. Найдите угол наклона касательной к графику
функции в точке с абсциссой х =0,25:
1) у =4х2; 2) у =-4х2.
Ответ: а) 1350; б) 450.
46. Найдите
первообразных функций: 1) х; 2) х3; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
Ответ: а)
![]() +С; б)
+С; б) ![]() +С; в)
+С; в) ![]() +С; г)
+С; г) ![]() д)
д) ![]() е) -
е) -![]() .
.
47. Для функции найдите первообразную, график
которой проходит через данную точку (х0;у0): 1)
f(х)=sinх, О(0;0); 2) f(х)=соsх,
М(![]() ; 1); 3)
f(х)=
; 1); 3)
f(х)=![]() ; М(
; М(![]() ; 0).
; 0).
Ответ: а) F(х) = tqх – 1; б) F(х) = - соsх + 1; в) F(х) = sinх +![]() .
.
48. Найдите первообразную функции: 2х+1.
Ответ: 1) х(х+1)+С; 2) х2+1+С; 3)
х(х-1)+С; 4) х2+2х+С.
49. Назвать методы интегрирования данных интегралов:
1) ![]() dx; а) интегрирование рациональных
выражений;
dx; а) интегрирование рациональных
выражений;
2) ![]() dx; б)
метод замены переменной;
dx; б)
метод замены переменной;
3) ![]() dx; в)
интегрирование тригонометрических
dx; в)
интегрирование тригонометрических
функций;
4) ![]() dx; г)
непосредственное интегрирование;
dx; г)
непосредственное интегрирование;
5) ![]() ; д) метод
интегрирования по частям.
; д) метод
интегрирования по частям.
50. Предложенные формулы позволяют:
1) S = ![]() а) определить объем тела
вращения вокруг оси ОУ;
а) определить объем тела
вращения вокруг оси ОУ;
2)
V = π ![]() б) определить объем продукции,
произведенной за промежуток времени.
б) определить объем продукции,
произведенной за промежуток времени.
3) V = π ![]() в) определить объем тела вращения
вокруг
в) определить объем тела вращения
вокруг
оси
ОХ.
4) Q(![]() ) =
) = ![]() г) вычислить площадь фигуры.
г) вычислить площадь фигуры.
51. Вычислить интеграл:
1) ![]() ; а)
; а)
![]() ; б) 3; в) 3 –
; б) 3; в) 3 – ![]() ;
;
2) ![]() ; а)1;
б)0; в)π;
; а)1;
б)0; в)π;
3) ![]() а)
а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
52. Что
больше: ![]()
Ответ: ![]()
53. Вычислить площадь фигуры, ограниченной линиями:
у=7х-х2-10 и осью ОХ.
Ответ: 1)14; 2) 64; 3) 4; 4) 4![]() .
.
54. Вычислить площадь фигуры, ограниченной линиями:
у=соsх, х= -![]() , х=
, х=![]() и у=0.
и у=0.
Ответ: 1) 1; 2) -1; 3) 1,5; 4) 2.
55. Вычислить площадь фигуры, ограниченной линиями:
1) у = х3, у = 0, х = -1, х = 1; а)
2;
2) у = х2 – 4х и осью абсцисс; б)
0,5;
3) у = ![]() , у = 0, х = -
, у = 0, х = - ![]() π; х = π; в)
10
π; х = π; в)
10![]() ;
;
4) у = ![]() у = 0; х = 0, х = π; г)
3,5.
у = 0; х = 0, х = π; г)
3,5.
56. Установить соответствие между приведенными
дифференциальными уравнениями первого порядка и их типами:
1)у
= ![]() ; а)
с разделяющимися переменными;
; а)
с разделяющимися переменными;
![]() б)
линейное;
б)
линейное;
![]() в)однородное.
в)однородное.
57. Сколько четырехзначных чисел можно составить из
цифр 0, 1, 2, 3, 4, 5, если:
1) ни одна цифра не повторяется; а) 1080;
2) цифры повторяются; б) 540;
3) нечетные числа могут повторяться; в) 300.
58. Сколькими способами можно составить комиссию из
трех супружеских пар, если:
1) комиссию можно составить произвольно; а) 32;
2) в комиссию не входят супруги; б) 56.
59. Игральную кость подбрасывают один раз. Найти
вероятность событий:
1) появление четного числа очков; а) ![]() ;
;
2) появление не менее пяти очков; б) ![]() ;
;
3) появление не более пяти очков; в) ![]() .
.
60. Девять различных книг расставлены наудачу на
одной полке. Найти вероятность того, что четыре определенные книги окажутся
постав ленными рядом.
Ответ: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.