
№ 1 (інструктивні
матеріали ). Завдання 1
Дана система лінійних рівнянь. 1. а) розв'язати
її за правилом Крамера; б) обчислити визначник третього порядка двома методами.
2. Перевірити отримане рішення.
1.1  1.2
1.2
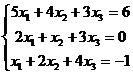
1.3 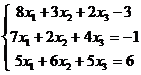 1.4
1.4 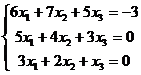
1.5 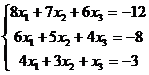 1.6
1.6
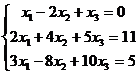
1.7  1.8
1.8
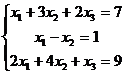
1.9  1.10
1.10

Практичне заняття № 2
Тема: Розв`язування вправ на складання прямих та площині.
Визначення кута між прямими на площині,
відстані від точки до прямої. Залікове заняття по темах першого модуля.
Повторення питань теми:
1.
Пряма
лінія т її рівняння на площині і в просторі:
-
Відстань
між двома точками;
-
Поділ
відрізка в даному відношенні;
-
Поняття
рівняння лінії на площині;
-
Рівняння
прямої лінії з кутовим коефіцієнтом;
-
Рівняння
прямої, що проходить через дану точку із заданим направляючим вектором;
-
Рівняння
прямої, що проходить через дві точки;
-
Рівняння
прямої, яке проходить через дану точку із заданим нормальним вектором;
-
Загальне
рівняння прямої та його дослідження;
-
Рівняння
прямої у відрізках;
-
Рівняння пучка прямих;
-
Обчислення
кута між двома прямими;
-
Умова
паралельності двох прямих;
-
Умова
перпендикулярності двох прямих;
2.
Криві
другого порядку:
-
Коло,
його рівняння;
-
Еліпс,
його рівняння, основні параметри;
-
Гіпербола,
її рівняння, основні параметри;
-
Парабола,
її рівняння, основні параметри.
Колективне виконування вправ:





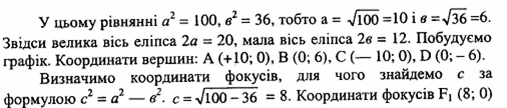
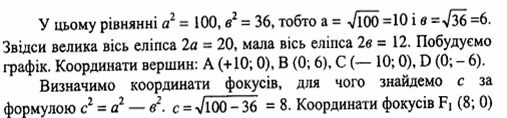


Самостійне виконування завдань
(згідно варіанта)
Завдання № 3 Обчислити роботу силу при переміщенні матеріальної крапки з
положення А в положення В.
3.1 А(3-3, 1); В(2-1,0); ![]() (1,2-4). 3.6
А(2,3,4); В(-3,0,5);
(1,2-4). 3.6
А(2,3,4); В(-3,0,5); ![]() (2-3,1);
(2-3,1);
3.2 А(2-1,-3); В(0,4,5); ![]() (3,3-1); 3.7
А(1,3,5); В(-3,0,7);
(3,3-1); 3.7
А(1,3,5); В(-3,0,7); ![]() (-1,3,3);
(-1,3,3);
3.3 А(-1,2,3); В(0-3,6); ![]() (2-2,2); 3.8 А(2,1,1);
В(-2,1,3);
(2-2,2); 3.8 А(2,1,1);
В(-2,1,3); ![]() (3-1,1);
(3-1,1);
3.4 А(-1,4,1); В(3,0,3); ![]() (1-1,4); 3.9
А(2,1,3); В(0,2,1);
(1-1,4); 3.9
А(2,1,3); В(0,2,1); ![]() (-1,2,3);
(-1,2,3);
3.5 А(-2,1,3); В(5,3,0); ![]() (5-1,3); 3.10
А(2-1,3); В(1,3,0);
(5-1,3); 3.10
А(2-1,3); В(1,3,0); ![]() (2-2,3).
(2-2,3).
Відповіді. 3.1 А=7; 3.2 А = 1; 3.3 А = 18; 3.4 А = 16; 3.5 А = 24; 3.6 А =
0; 3.7 А = 1; 3.8 А = -10; 3.9 А = -2; 3.10 А = -19.
Завдання № 4. Обчислити площу трикутника вершинам в крапках А, В, С.
4.1 А, В(2,2,1); С(-1,0,1); Відповідь:
S = 9.354.
4.2 А(-4,2,6); В(2-3,0); С(-10,5,8) Відповідь:
S = 14,0
4.3 А(7,2,4); В(7-1,-2); С(3,3,1) Відповідь:
S = 15,37
4.4 А(2,1,4); В(-1,5,-2); С(-7,-3,2) Відповідь:
S = 37,528
4.5 А(-1,-5,2); В(-6,0-3); С(3,6-3) Відповідь:
S = 46,233
4.6 А(0-1,-1); В(-2,3,5); С(1-5,-9) Відповідь:
S = 6,708
4.7 А( 5,2,0); В(2,5,0); С(1,2,4) Відповідь:
S = 10,392
4.8 А(2-1,-2); В(1,2,1); С(5,0-6) Відповідь:
S = 9,354
4.9 А(-2,0,-4); В(-1,7,1); С(4-8,-4) Відповідь:
S = 35,355
4.10 А(14,4,5); В(-5,-3,2); С(-2,-6,-3) Відповідь:
S = 66,287.
Завдання № 5. Обчислити об'єм трикутної піраміди з вершинами в крапках А,
В, З, Д.
А(1,2,0); В(3,0-3); С(5,2,6); Д(8,4-9)
А(2-1,2); В(1,2-1); С(3,2,1); Д(-4,2,5)
А(1,1,2); В(-1,1,3); С(2-2,4); Д(-1,0-2)
А(2,3,1); В(4,1-2); С(6,3,7); Д(7,5-3).
А(1,1-1); В(2,3,1); С(3,2,1); Д(5,9-8)
А(1,5-7); В(1,5-4); С(-2,7,3); Д(-4,8-12)
А(-3,4,-7); В(1,5-4); С(-5,-2,0); Д(2,5,4)
А(-1,2,-3); В(4-1,0); С(2,1-2); Д(3,4,5)
А(-4,-1,3); В(-2,1,0); С(0-5,1);
Д(3,2-6)
А(1-1,1); В(-2,0,3); С(2,1-1); Д(2-2,-4).
Відповіді: 5.1 V = 34. 5.2 V = 11. 5.3 V = ![]() . 5.4 V =
. 5.4 V = ![]() . 5.5 V =
. 5.5 V = ![]() . 5.6 V =
. 5.6 V = ![]() . 5.7 V =
. 5.7 V = ![]() . 5.8 V =
. 5.8 V = ![]() . 5.9 V =
. 5.9 V = ![]() . 5.10 V =
. 5.10 V = ![]() .
.
Завдання № 6. Задані пряма L і точка М. Потрібна:
а) обчислити відстань p(М, L) від точки М до прямій; б) написати рівняння
прямої L1, що проходить через точку МА перпендикулярно прямій
L, в) написати рівняння прямої L2, що проходить через точку М
паралельно прямій L; г) побудувати прямі L, L1, L2.
6.3 L: x-2y-4 = 0, M(1,2). 6.4 L: 2x-y-4 =
6.5 L: 3x-2y+6 =
6.7 L: 3x+4y-12 =
6.9 L: x+2y+2 =
Завдання № 7. Дано чотири крапки: М1, М2,
М3, М0. Потрібний: а) написати рівняння площини Р, що
проходить через точки М1, М2 і М3; би) перетворити отримане
рівняння площини Р в рівняння площини у відрізках і побудувати її; у) знайти
відстань р(М0, Р) від точки М0 до площини Р.
7.1 М1 (1,3,0), М2 (4-1,2), М3 (3,0,1), М0(4,3,0).
7.2
М1 (-2,-1,-1), М2 (0,3,2), М3 (3,1-4), М0(-21,20,-16).
7.3
М1 (-3,-5,-6), М2 (2,1-4), М3 (0-3,-1), М0(3,6,68).
7.4
М1 (2-4,-3), М2 (5-6,0), М3 (-1,3,-3), М0(2-10,8).
7.5
М1 (1-1,2), М2 (2,1,2), М3 (1,1,4), М0(-3,2,7).
7.6
М1 (1,3,6), М2 (2,2,1), М3 (-1,0,1), М0(5-4,5).
7.7
М1 (-4,2,6), М2 (2-3,0), М3 (-10,5,8), М0(-12,1,8).
7.8
М1 (7,2,4), М2 (7-1,-2), М3 (-5,-2,-1), М0(10,1,8).
7.9
М1 (2,1,4), М2 (3,5-2), М3 (-7,-3,2), М0
(-3,1,8).
7.10
М1 (-1,-5,2), М2
(-6,0,3), М3 (3,6-3), М0(10-8,-7).
Завдання № 8. Дано три рівняння кривих другого порядку Г1, Г2,
Г3. Потрібний: привести рівняння до канонічного вигляду, визначити
тип і побудувати ці криві.
8.1 Г1: 4х2 + 81у2 = 324; Г2: 16у2 – 4х2
= 64; Г3: 5х2 +
9у2 – 30х + 18у + 9 = 0
8.2 Г1: 9у2 – 49х2 = 441; Г2:
9х2 + 36у2 = 324; Г3: 16х2 – 9у2
= 64х + 54у = 161.
8.3 Г1: 4х2 + 9у2 = 36; Г2: 25х2
– 4у2 = 100; Г3: 16х2 + 25у2 + 32х = 100у + 284.
8.4 Г1: 16х2 – 9у2 = 144; Г2:
25х2 + 9у2 – 225 = 0; Г3: 4х2 + 3у2
= 8х – 12у + 32.
8.5 Г1: 36х2+9у2–324 = 0; Г2:
25х2–16у2 = 400; Г3: 9х2–16у2+ 90х+32у–367 = 0.
8.6 Г1: 16х2+25у2 – 400=0; Г2:
25х2-9у2=225; Г3: 4х2 – 8х-у+7=0.
8.7 Г1: 4х2+16у2 – 64=0; Г2:
81х2-4у2 = 324; Г3: 16х2 – 9у2
– 64х + 18у – 89 = 0.
8.8 Г1: 4х2 – 25у2 – 100=0; Г2:
9х2 +16у2=144; Г3: 2у2-12у –х+14=0.
8.9 Г1: 9х2 – 4у2 = 36; Г2: 16х2-25у2
– 400=0; Г3: 4х2 – у2 – 8х –6у –9=0.
8.10 Г1: 9у2 +49х2 = 441; Г2:
4у2 – х2 – 4=0; Г3: 9х2
– 4у2 – 36х+24у=0.
Практичне заняття № 3
Тема: Розкриття найпростіших невизначеностей. Важливі границі.
Натуральні логарифми
Повторення питань теми:
1.
Означення функції, основні властивості функції;
неперервні та перервні функції (навести приклади).
2.
Поняття
границі функції.
3.
Основні
теореми про границі.
4.
Перелічити
основні невизначеності та їх усунення.
5.
Важливі
границі. Поняття натуральних логарифмів.
Колективне виконування вправ:
1.
Обчислити:
-
![]() ;
;
-
![]() ;
;
-
![]() ;
;
-
![]()

Самостійне виконування завдань (згідно варіанта)
Завдання № 9. Знайти межі функцій (у пункті С скористатися властивістю
еквівалентності).
9.1 а) 
9.2 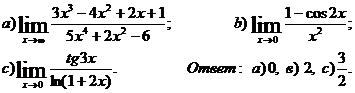
9.3 
9.4 
9.5 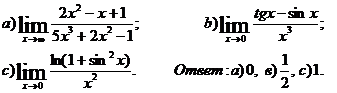
9.6 
9.7 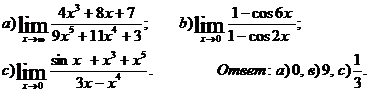
9.8 
9.9 
9.10 
Завдання № 10. Задана функція f(x). Знайти точку розриву функції і
досліджувати її характер.
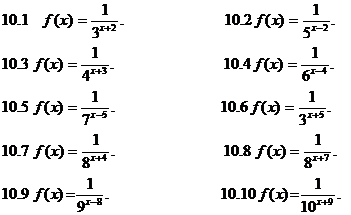
Практичне заняття № 4
Тема: Похідна. Техніка диференціювання
Повторення питань теми:
1.
Означення
похідної; символічний вигляд похідної.
2.
Геометричний,
фізичний та хімічний сенси похідної.
3.
Рівняння
дотичної (нормалі) до графіка функції.
4.
Основні
формули диференціювання; правила диференціювання.
5.
Похідна
складеної функції.
Колективне виконування вправ:


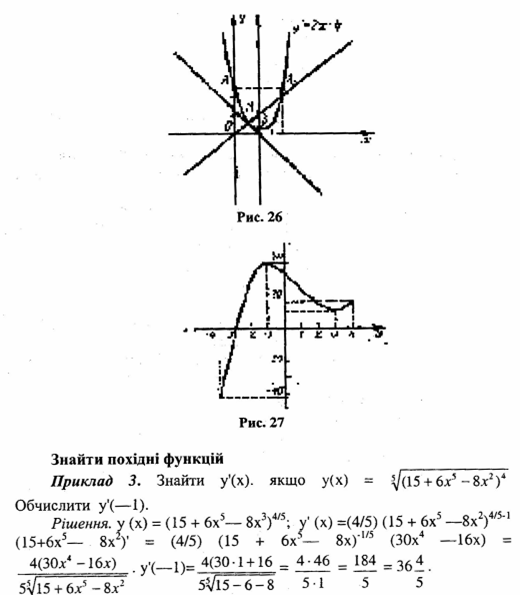
Самостійне виконування завдань №№ 11, 12, (б-додаткове
завдання) (згідно свого варіанта)
Завдання № 11. Знайти похідну
у`(х), якщо:
11.1 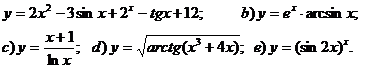
11.2 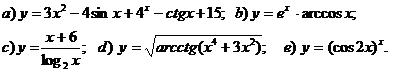
11.3 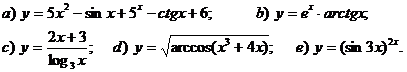
11.4 
11.5 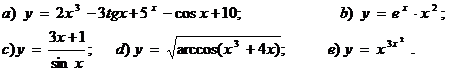
11.6 ![]()
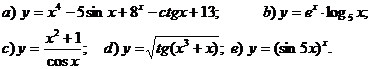
11.7 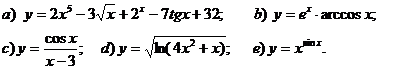
11.8 
11.9 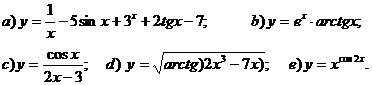
11.10 
Завдання № 12.
Знайти першу і другу похідні функції , якщо:
12.1 ![]()
12.2 ![]()
12.3 ![]()
12.4 ![]()
12.5 
12.6 ![]()
12.7 ![]()
12.8 ![]()
12.9 ![]()
12.10 ![]()
Практичне заняття № 5
Тема: Поняття диференціала функції та його застосування.
Повторення питань теми:
1.
Дайте
означення диференціала функції.
2.
Чому
дорівнює диференціал незалежної змінної (аргументу)?
3.
За
яким правилом знаходять диференціал функції?
4.
У
чому полягає геометричний сенс диференціала функції?
5.
Як
використовують диференціал функції в наближених обчисленнях?
Колективне виконування вправ:
1.
Знайти
диференціали функцій: а) у=(2х2-1)·(3-5х2); б) V=lnsin32φ.
2.
Обчислити значення диференціала функції S=√t2+9 при зміні t від 4 до 4, 025.
3.
Обчислити
наближене значення приросту функції у=(1+х-х3)2 при зміні х від 3 до 2, 998.
4.
Знайти наближене
значення: а) √1,005; б) 3√0,9843.
5.
Обчислити наближено:
![]()

Самотійне
виконування завдань (згідно
свого варіанта)
1.
В №1 (9.41; 9.44; 9,47). В №2 (9.42;
9,45; 9,48). В №3 (9.43; 9,46; 9,49).
2.
КЗ №9 (стор. 224).
3.
Тест 9 (стор. 225).
Практичне заняття № 6
Тема: Розв׳язування вправ на застосування похідної для дослідження
функції.. Екстремум функції. Необхідна і достатня умова існування екстремуму
функції. Загальні дослідження функції та побудова графіка функції.
Розв’язування вправ на дослідження функції за допомогою похідної та побудову
графіків функцій.
Повторення питань теми:
1.
Умови зростання та
убування функції.
2.
Необхідні та
достатні умови існування екстремуму функції.
3.
Умови існування
крапки перетину графіка функції.
4.
Схема дослідження
функції на екстремум.
5.
Необхідні та
достатні умови опуклості та угнутості графіка функції.
6.
Загальна схема
дослідження функції та побудови графіка функції.
7.
Правило Лопіталя про усунення невизначеностей,
що потребують додаткових досліджень.
8. Приклади застосування правила Лопіталя.
9. Приклади розв`язування завдань на
максимум та мінімум з економічним сенсом.
10.
Алгоритм находження
найбільшого та найменшого значень функції.
Виконання вправ:
Колективне:
1)
Практикум з вищої
математики для економістів № 8.100-8.104, 8.108-8.110.
2) Практикум з вищої математики для економістів № 8.9-8.13, 8.14.
3) Практикум з вищої математики для економістів № 8.37-8.40, 8.61-
8.69, 8.75-8.8.76.
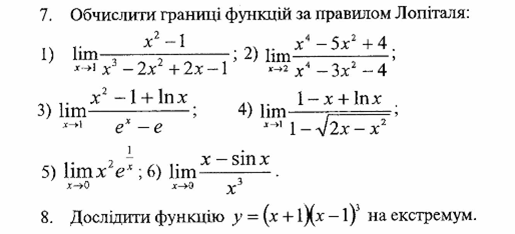

Самостійне виконування завдань згідно указаного варіанту
1.
№11А (інструктивні матеріали ).
2.
Завдання № 101-120.(домашня КР)
У завданнях 101-120 досліджувати дані
функції методами диференціального числення і побудувати їх графіки. Дослідження
функції рекомендується перевірити по наступній схемі: 1) знайти область
визначення функції; 2) досліджувати функцію на безперервність; 3) визначити, чи
є дана функція парною, непарною; 4) знайти інтервали зростання і убування
функції і точки її екстремуму; 5) знайти інтервали опуклості і угнутості
графіка функції і точки перегину; 6) знайти асимптоти графіка функції.
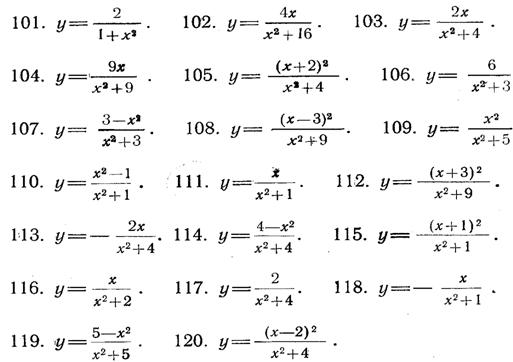
Практичне заняття № 7
Тема: Найпростіші методи інтегрування. Розв’язування вправ на
інтегрування .
Повторення питань теми:
1. Дати означення первісної, назвати основні властивості.
2. Невизначений інтеграл та його властивості.
3. Таблиця основних невизначених інтегралів.
4. В якому разі можна використовувати безпосереднє інтегрування?
5. В чому полягає суттєвість інтегрування
методом підстановки?
6. Напишіть формулу інтегрування за
частинами, в якому сенсі використовують
формулу інтегрування за частинами?
Виконання вправ :
Колективне:
1. Практикум з вищої математики для економістів тест
№10.(аналіз виконання тесту, основні помилки, робота над ними).
2. Практикум з вищої математики для економістів глава 10
(1-3)


Самостійне виконування завдань згідно указаного варіанту
( завдання №16,17)
ЗАВДАННЯ № 16.
Знайти невизначені інтеграли:
16.1
![]()
16.2
![]()
16.3
![]()
16.4

16.5
![]()
ЗАВДАННЯ № 17.
Використовуючи формули інтеграції
по частинах, обчислити інтеграли.
17.1
![]()
17.2
![]()
17.3
![]()
17.4
![]()
17.5
![]()
Практичне заняття № 8
Тема: Розв’язування
вправ на обчислення визначеного інтеграла за
формулою Ньютона-Лейбніца.
Розв’язування геометричних, фізичних та технічних задач за допомогою
визначеного інтеграла.
Повторення питань теми:








Самостійне виконування завдань згідно указаного варіанту
Завдання № 20.
Обчислити певні інтеграли:
20.1 
20.2 
20.3 
20.4 
20.5 
2. Завдання № 21.
Обчислити невласні інтеграли або
встановити їх збіжність чи розбіжність.
21.1 
21.2 
21.3 
21.4 
21.5 
Практичне заняття № 9
Тема: Безпосереднє обчислення ймовірності подій. Теорема
додавання ймовірностей та теорема множення ймовірностей. Повторення незалежних
випробувань. Формула Бернуллі. Граничні теореми. Формула Пуассона.
Повторення питань теми:
1.
Елементи
комбінаторики.
2.
Класичне та
геометричне означення ймовірності.
3.
Теореми додавання
та множення ймовірностей.
4.
Умовна ймовірність.
5.
Формула повної
ймовірності.
6.
Формули Байєса.
7.
Схема та формула
Бернуллі.
8.
Граничні теореми в
схемі Бернуллі.
9.
Послідовності
випробувань з різними ймовірностями.
10.
Випадкові величини. Закони розподілу.
11.
Числові характеристики випадкових величин.
12.
Нерівність Чебишова. Закон великих чисел.
13.
Центральна гранична теорема. Ймовірності
процеси та їх застосування.
Колективне розв’язування вправ










Самостійне виконування завдань згідно указаного варіанту
Міхайленко В.М., Теренчук С.А., Кубайчук О.О. «Теорія ймовірностей,
ймовірнісні процеси та математична статистика» (збірник задач).
1) стор.13-14; 2) стор.18-21; 3)
стор. 28-29; 4) стор. 46-48; 5) стор. 57-60.
Практичне заняття № 10
Тема: Розв’язування
вправ на статистичний розподіл
вибірки та його характеристик. Залікове заняття з тем другого модуля.
Повторення питань теми:
1.
Математична
статистика та її задачі.
2.
Вибірка.
Статистичний розподіл.
3.
Емпірична
функція розподілу.
4.
Числові
характеристики вибіркової сукупності.
5.
Довірчі
інтервали.
6.
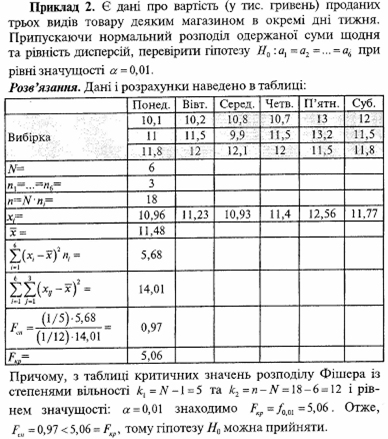
Статистичні
гіпотези.
7.
Критерії
Стьюдента, Фішера, Пірсона.
Колективне розв’язування вправ




Приклади на перевірку гіпотез


Самостійне виконування завдань згідно указаного варіанту
№
1


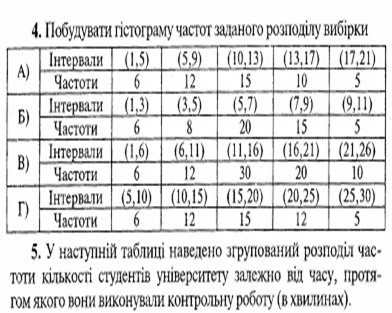

№
2
