Высшая математика

ОТДЕЛЬНОЕ ПОДРАЗДЕЛЕНИЕ НАЦИОНАЛЬНОГО УНИВЕРСИТЕТА БИОРЕСУРСОВ И ПРИРОДОПОЛЬЗОВАНИЯ УКРАИНЫ

«КРЫМСКИЙ АГРОПРОМЫШЛЕННЫЙ КОЛЛЕДЖ»

 

Материалы для директорской контрольной

работы по дисциплине «Высшая математика»

Преподаватель: Черемисина Л.Н.

Аннотация

на контрольную работу по дисциплине «Высшая математика».

  В контрольную работу включены задачи и тесты-задания по курсу  «Высшая математика», изученные на момент проведения работы из разделов: «Линейная алгебра», «Векторная алгебра и аналитическая геометрия», «Дифференциальное исчисление», «Интегральное исчисление». Работа составлена по 10 вариантам. Задания вариантов равноценны. Каждый вариант содержит по пять заданий из разных разделов курса. Работа даст возможность провести промежуточный контроль по дисциплине и выявить пробелы и упущения при изучении курса «Высшая математика».

 

Критерии

оценивания контрольной работы

по дисциплине «Высшая математика»

         Оценка «отлично»  выставляется в том случае, если выполнены правильно все пять заданий контрольной работы, получены во всех заданиях верные ответы, построены необходимые чертежи и рисунки; есть пояснения во всех заданиях и ссылки на теоретический материал.

         Оценка «хорошо»  выставляется в том случае, если выполнены правильно все пять заданий контрольной работы, получены во всех заданиях верные ответы, построены не все необходимые чертежи и рисунки;  пояснения в1-2 заданиях и ссылки на теоретический материал отсутстствуют или недостаточные. Оценка «хорошо»  может быть выставлена, если выполнены правильно четыре задания контрольной работы с подробными пояснениями и построениями.

         Оценка «удовлетворительно»  выставляется в том случае, если выполнены правильно все пять заданий контрольной работы,  во всех заданиях верные ответы, но  нет в работе необходимых чертежей и рисунков;  пояснения  и ссылки на теоретический материал отсутстствуют или недостаточные. Оценка «удовлетворительно»  может быть выставлена, если выполнены правильно три задания контрольной работы с подробными пояснениями и построениями.

         Оценка «неудовлетворительно»  выставляется в том случае, если выполнены правильно одно или два задания контрольной работы. Оценка «неудовлетворительно»  может быть выставлена, если выполнены правильно три задания контрольной работы, но без подробных пояснений и построений.

 

Вариант 1

1.     Дана система линейных уравнений. Решить ее по правилу Крамера. Проверить полученное решение.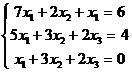

 

2.     Заданы прямая L и точка М.

Требуется: а) вычислить расстояние d от точки М до прямой; б) написать уравнение прямой L1, проходящей через точку М перпендикулярно прямой L, в) написать уравнение прямой L2, проходящей через точку М параллельно прямой L; г) построить прямые L, L1, L2.

                             L: x+3y+3 = 0,  M(1,1).

       3.  Векторы: а) коллинеарные; б) перпендикулярные; в) имеют равные длины:

1) (1; -2; 6) и (-1; 6; 2);

2)  (-5; 2; 3) и (10; -4; -6);

3) (-3; 2; 1) и (4; 6; 0).

        4.   Установить соответствие между графиками функций у = f (1, 2, 3) и графиками их производныху' = f (а, б. в):

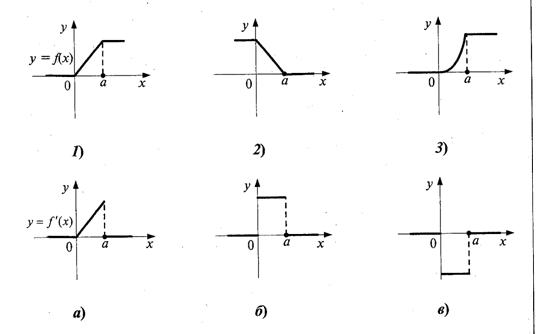
5. Найти совокупность всех первообразных функции у= sin3х+2соs.

Преподаватель:            Черемисина  Л.Н.

 

                                                          Вариант 2

1.     Дана система линейных уравнений. Решить ее методом Гаусса. Проверить полученное решение. 

2.     Вычислить площадь треугольника с вершинам в точках: А, В, С.

  А(1,3,6), В(2,2,1); С (-1,0,1);

3. При каком значении k векторы являются коллинеарными:

1.  (1;-1;1) и (k;3;-3);                               а) -24;

2.  (4;6;k) и (;-       ;3);                                  б) -1;

3.  (-2k; 2k+2; -2) и (3;-4; 1);                          в) -3;

4.  (2k; 3; 4) и (4;-6; -8);                                 г) 3.

4.  Предложенные формулы позволяют:

1) у' (х) = ;                        а) найти дифференциал функции ;

2) dy = y'(x)dx;                                б) дать понятие производной;

3) (x + ∆x) ≈ (x0) + ´(x0)dx;             в) найти угол наклона касательной;

4) y'(x0) = tq;                                 г) составить уравнение касательной;

5) у – у0 = y'(x0)∙(х-х0);                    д) найти приближенное значение функции.

5.  Что больше:

Ответ:

 

                  

                                       

 

Вариант 3

1.     Дана система линейных уравнений. Решить ее  методом обратной матрицы. Проверить полученное решение.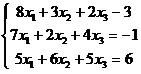

2.     Вычислить объем треугольной пирамиды с вершинами в точках: А, В, С, Д.

А(1,2,0); В(3,0,-3); С(5,2,6); Д(8,4,-9)

3.      Чему равно скалярное произведение векторов  если:

1)  и коллинеарные и одинаково направленные;           а) х2+у2+z2;

2)  и противоположные;                                                  б) х1х2+у1у2+z1z2;

3)  и                                           в) -х2-у2-z2;

4)  иравные?                                                           г) 0.

      4.  Составить уравнение касательной к графику функции у = 4х – х2  в точке х0=3.

Ответ: у = кх+в, где к = …; в = … .

       5. Найти производную у`, если: а) у = соsх; б) у =.

 

 

 

Вариант 4

1.     Дана система линейных уравнений. Решить ее одним из методов. Проверить полученное решение.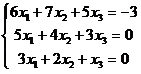

2.     Вычислить площадь треугольника с вершинам в точках: А, В, С.   А(-4,2,6); В(2,-3,0); С(-10,5,8)

3.      Найдите соответствие между заданными прямыми и видами  этих прямых:

1) Ах + Ву + С = 0;                    а) уравнение прямой в общем виде;

2)  +  = 1;                                           б) уравнение прямой, заданной 2мя            точками;

3)  = ;                              в) уравнение в отрезках;

4) А∙(х -х0)+ В∙(у – у0) + С = 0;           г) уравнение прямой, заданной с помощью точки и направляющего вектора;

5)  = ;                                д) уравнение  пучка прямых;

6) у – у0 = k ∙( х – х0);                е) уравнение прямой, заданной с помощью точки и перпендикулярного вектора;

 

4.     Назовите некоторые методы раскрытия неопределенностей типа: 2

 

5.     Найти наибольшее значение функции у = f(x) на отрезке [a; b]. 

f(х)=х3-12х+7, [0;3]

 

 

 

 

 

Вариант 5

1.     Дана система линейных уравнений. Решить ее одним  методом Гаусса. Проверить полученное решение.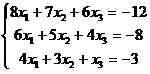

2.     Вычислить объем треугольной пирамиды с вершинами в точках: А, В, С, Д.

А(2,-1,2); В(1,2,-1); С(3,2,1); Д(-4,2,5)

3.      Какие из заданных прямых перпендикулярны прямой 2х – у + 3 = 0;

1)    4х +8у + 17 = 0; 2) 4х -8у – 11 = 0; 3) у = -   4) у = -2х – 7; 5)

4.      Найти пределы функций:

1) ;                             а) 2;

2) ;                                 б) ;

3)                                 в) 1,5.

4)                          г)

        5. Найти наибольшее значение функции у = f(x) на отрезке [a; b]. 

         f(x)=х4+4х, [-2;2]

 

                                      

 

 

Вариант 6

1.     Дана система линейных уравнений. Решить ее одним  методом Гаусса. Проверить полученное решение.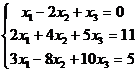

2.     Вычислить площадь треугольника с вершинам в точках: А, В, С. А(7,2,4); В(7,-1,-2); С(3,3,1)

3.      Найти соответствие между утверждениями относительно двух плоскостей

А1х + В1у + С1z +D1 =0 (1), А2х + В2у + С2z +D2 =0 (2), прямой    =  =  и их признаками:

1)    плоскости параллельны;                                    а) А1В2 + С1С2 =0;

2)    плоскости перпендикулярны;                            б)  =  =

3)    плоскость (1) и прямая параллельны;              в) А1m + В1n + С1р =0;

4)    плоскость (1) и прямая перпендикулярны;      г) = =

  4.  Правило Лопиталя не может быть применено для нахождения предела:

1) ;        2) ;      3);    4)

 

5. Найти наибольшее значение функции у = f(x) на отрезке [a; b]. 

         f(x)=х4-4х, [0;2]

 

 

 

 

Вариант 7

1.     Дана система линейных уравнений. Решить ее одним  из методов. Проверить полученное решение.

2.     Вычислить объем треугольной пирамиды с вершинами в точках: А, В, С, Д.

А(1,1,2); В(-1,1,3); С(2,-2,4); Д(-1,0-2)

3.      Найдите соответствие между заданными уравнениями и видами кривых второго порядка:

1) 3х2 – 4у2 = 12 ;                                     а) уравнение эллипса;

2) х2 + у2 + 10х – 4у – 20 = 0;                  б) уравнение параболы;

3) 5х2 + 4у2 = 20;                                      в) уравнение окружности;

4) х2 = 8у;                                        г) уравнение гиперболы.

       4.   Среди перечисленных функций убывает на всей области определения

функция:

1)    у =  2) у = ; 3) у =  4) у = х3 – х2; 5) у = х3 + х2.

5.    Найти промежутки выпуклости и вогнутости графика функции и точки перегиба:  у=12х-4х3.

 

 

 

Вариант 8

1.Дана система линейных уравнений. Решить ее одним  из методов. Проверить полученное решение.

2. Вычислить площадь треугольника с вершинам в точках: А, В, С. А(2,1,4); В(-1,5,-2); С(-7,-3,2).

3.  Привести кривые второго порядка к каноническому виду и указать вид кривой:

1) х2 =                       а)                   А) уравнение окружности;

2) 5х2 – 3у2 = 75;          б) у = 8х2;                     Б) уравнение параболы;

3) х2 + у2 – 4х + 6у – 23 = 0; в)                   В) уравнение гиперболы;

4) 4х2 + 9у2 = 144;                 г) (х-2)2+ (у+3)2 = 46;   Г) уравнение эллипса.

    4.  Выяснить, какое из приведенных утверждений является неверным:

1) в точке экстремума  производная функции равна  нулю или не существует;

2) в точке экстремума  функция меняет знак;

3) в точке экстремума  производная меняет знак;

4) в точке, в которой проиводная равна нулю или не существует, может не быть экстремума?

    5. Найти наибольшее значение функции у = f(x) на отрезке [a; b]. 

         f(x)=4х3-12х, [-1;2]

 

 

 

 

Вариант 9

1.     Дана система линейных уравнений. Решить ее одним  из методов. Проверить полученное решение.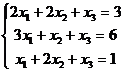

2.     Вычислить объем треугольной пирамиды с вершинами в точках: А, В, С, Д.

А(2,3,1); В(4,1,-2); С(6,3,7); Д(7,5,-3).

3.      Выясните,  какие из функций являются сложными:

1) у = ;    2) у = ()х; 3) у =                  4) у =

      4.  Найти производные функций:

1) у = (3;                               а)  -

2) у = + ;                       б) ;

3) у = ;                                   в) + ;

4) у = х∙ – ;                         г) 3(1 + )2 .

      5. Найти промежутки выпуклости и вогнутости графика функции и точки перегиба: 

         f(x)=3х3-9х.

 

 

 

Вариант 10

1.     Дана система линейных уравнений. Решить ее одним  из методов. Проверить полученное решение.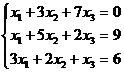

2.     Заданы прямая L и точка М.

Требуется: а) вычислить расстояние d от точки М до прямой; б) написать уравнение прямой L1, проходящей через точку М перпендикулярно прямой L, в) написать уравнение прямой L2, проходящей через точку М параллельно прямой L; г) построить прямые L, L1, L2.

 L = x-2y – 2 = 0, M (1,1).    

3.     Выясните, какие из функций заданы неявно:

1) у =      2) у =        3) х – у = х∙у.

 

4.      По графику функции определить:

 

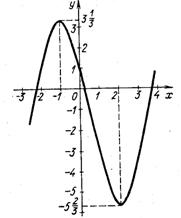
1) промежутки возрастания функции;                       а) (-1;2);

2) промежутки убывания функции;                           б) (-

3) абсциссу точки максимума;                                   в) 2;

4) абсциссу точки минимума;                                    г) -1.

     5. Найти наибольшее значение функции у = f(x) на отрезке [a; b]. 

         f(x)=3х3-4,5х2, [-2;2]