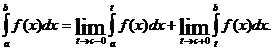ЛЕКЦІЯ № 1

Тема: Вступ. Предмет і методи математики. Зв’язок з практикою. Короткі відомості з історії математики. Матриці, визначники другого та третього порядку. Властивості визначників. Застосування визначників до розв’язання систем лінійних рівнянь. Повторення алгебри, тригонометрії, основних елементарних функцій. Видача типового розрахунку по елементарній математиці.

Питання лекції:

1.Вступна бесіда про курс вищої математики.

2. Предмет і методи математики, зв`язок математики з практикою, природничими науками, економікою. Поняття математичного моделювання.

3. Матриці, види матриць.

4. Визначники другого та третього порядку. Властивості визначників.

5. Застосування визначників до розв’язання систем лінійних рівнянь.

6. Повторення алгебри, тригонометрії, основних елементарних функцій. Видача типового розрахунку по елементарній математиці.

Вступна бесіда про курс вищої математики (кількість годин аудиторної та самостійної роботи, кількість модулів, модульно-рейтинговий підсумок, поточний та підсумкові види контролю, практичні заняття, список необхідної літератури).

Предмет та методи і завдання дисципліни «Вища математика»

Математика є універсальною наукою, яка широко застосовується у всіх сферах діяльності. На сучасному етапі роль математики в розвитку суспільства збільшується, потрібне підвищення математичної підготовки, особливо фахівців з економічного профілю. В процесі вивчення дисципліни студенти повинні придбати фундаментальні математичні знання з відповідними професійними напрямами, уміння працювати з великим масивом даних, обробляти статистичну інформацію, володіти обчислювальними навиками і так далі

Вивчення курсу вищої математики пов`язане з вивченням курсів математики і фізики в середній школі.

1. ЗАВДАННЯ КУРСУ:

- Вивчити основи аналітичної геометрії, лінійної алгебри, інтегрального і диференціального числення. Показати області застосування цих знань в економіці з упором на використання сучасної обчислювальної техніки. Підготувати студентів до вивчення дисциплін, що систематично використовують вищу математику і читаних на старших курсах.

2. КВАЛІФІКАЦІЙНІ ВИМОГИ ДО ЗАСВОЄННЯ

СТУДЕНТАМИ ПРОГРАМНОГО МАТЕРІАЛУ

2.1. ЗНАТИ:

- основні правила аналітичної геометрії, методи вирішення систем лінійних рівнянь алгебри. Розуміти зв'язок між такими поняттями, як число, вектор, матриця, лінійне перетворення.

- основні теореми і правила диференціального і інтегрального числення, області їх застосувань в економічній науці.

- основні теореми теорії диференціальних рівнянь і способи їх застосування для опису детермінованих процесів в економіці.

- основні правила наближених обчислень.

2.2. УМІТИ:

- складати математичні моделі конкретних планово-економічних завдань з використанням таких понять як власний вектор лінійного перетворення.

- складати диференціальні моделі поточних в часі економічних процесів.

- вирішувати оптимізаційні завдання в економіці.

- оцінювати межі застосовності математичних методів економічних розрахунках.

2.3. ОВОЛОДІВАТИ НАВИКАМИ

- оцінюючи погрішностей в обчисленнях.

- складання економічних прогнозів на основі математичних методів.

- вирішувати конкретні завдання і приклади курсу.

2.4. РОЗВИНУТИ ТВОРЧІ ЗДІБНОСТІ:

- у умінні складати абстрактну модель того або іншого процесу.

- у логічному науковому мисленні.

Матриці, приватні види матриць

Матрицею називається прямокутна таблиця чисел.

Матриця позначається круглими дужками з боків таблиці. Матриці також позначають великими латинськими буквами А, В, З, Е, Х.

Тут показані різні типи матриць. Матриця А – прямокутна, розмірністю (2 х 3); матриця В – квадратна, у неї число рядків рівне числу стовпців; матриця С складається з одного стовпця (матриця-стовпець). Є також діагональні матриці – це квадратні матриці, у яких всі елементи, окрім тих, що стоять в головній діагоналі, рівні нулю. Одиничні матриці – це діагональні матриці, у яких в головній діагоналі стоять одиниці. Наприклад

Тут Д – діагональна матриця; Е, I – одиничні матриці різної розмірності.

Визначником 2-го порядку, відповідним квадратній матриці А, називається число

Аналогічно, якщо

квадратна матриця 3-го порядку, то відповідним нею визначником 3-го порядку називається число

Наприклад

а)

Деякі властивості визначників:

1. Визначник рівний нулю, якщо:

а) рядок або стовпець складаються з нулів;

б) є два однакові ряди два рядки або два стовпці);

в) елементи паралельних рядів пропорційні.

2. Визначник не зміниться, якщо:

а) паралельні ряди поміняти місцями парне число разів;

б) до елементів одного ряду додати елементи іншого ряду, помножені на одне і теж число;

в) рядки зробити стовпцями, а стовпці – рядками (така операція називається транспонуванням визначника).

Мінор, доповнення алгебри

розкладання визначника по елементах ряду

Мінором М_IJ елементу а_IJ даного визначника називається визначник, отриманий з даного шляхом викреслювання рядка і стовпця, на перетині яких стоїть елемент а_IJ. Тут і – номер рядка, j – номер стовпця.

Наприклад, для елементу а₁₃ визначника ∆ мінор має вигляд:

Доповненням алгебри А_IJ елементу а_IJ називається мінор цього елементу, помножений на (-1) в ступені, рівній сумі номерів рядка і стовпця:

Кожен визначник ∆ може бути обчислений як сума творів елементів якого-небудь ряду на їх доповнення алгебри:

Формула (2.7) називається розкладанням визначника по елементах ряду. (ця формула називається теоремою Лапласа)

Системою лінійних рівнянь алгебри з трьома змінними називають ( 1 )

( 1 )

де х₁, х₂, х₃ – невідомі, а₁₁, а₂₂..., а₃₃ - коефіцієнти, а b₁, b₂, b₃ незалежні числа. Рішенням СЛР називають сукупність чисел Хn, яка задовольняє кожному з рівнянь системи.

Система називається сумісною, коли вона має рішення і несумісною - коли не має рішення. Якщо система має більш одного рішення, вона називається сумісною невизначеною.

2. Правило Крамера

Систему лінійних рівнянь алгебри

де х₁, х₂, х₃ – невідомі, а₁₁, а₁₂..., а₃₃ - коефіцієнти, а b₁, b₂, b₃– незалежні числа, можна вирішити за правилом Крамера, яке полягає в наступному:

- система має єдине рішення, якщо визначник системи не дорівнює 0

- само рішення визначається по формулах:

Визначник ∆ складається з коефіцієнтів, допоміжні визначники ∆1; ∆2; ∆3 виходять з ∆ шляхом заміни першого, другого і так далі стовпців стовпцем вільних членів:

Питання для самоперевірки.

1. Що називається матрицею ?

2. Основні види матриць.

3. Що називають визначником 2, 3, n-го порядків?

4. Назвіть основні властивості визначників.

5. Що називають мінором елемента матриці?

6. Що називають алгебраїчним доповненням елемента матриці?

7. Сформулюйте формулу розкладання визначника по елементах ряду. Як інакше називають дану формулу.

8. Запишіть розкладання визначника 3 порядку по елементах першої строки, другого стовпця.

9. Запишіть правило Крамера, в якому разі можна його використовувати ?

Домашнє завдання: Кремер М.Ш. «Вища математика для економістів» гл.1; 2.

ЛЕКЦІЯ № 2

ТЕМА: Предмет і метод аналітичної геометрії. Прямокутна система координат на площині. Найпростіші задачі аналітичної геометрії. Рівняння лінії на площині. Рівняння прямої з кутовим коефіцієнтом. Загальне рівняння прямої та його дослідження.

Питання лекції:

1. Вектори (основні визначення, поняття ).

2. Векторний простір. Лінійна залежність та незалежність векторів.

3. Векторний базис, прямокутні координати на площі та у просторі.

4. Лінійці операції над векторами.

5. Векторний твір векторів.

6.Змішаний твір трьох векторів.

7. Рівняння прямої на площині. Способи складання прямої на площині, різноманітні формули прямої на площині.

8. Формули для находження кута між прямими; відстані від точки до прямої.

Вектори. Колінеарність, компланарність та рівність векторів.

Вектором називається направлений відрізок або впорядкована пара крапок. Позначається

Два вектори називаються колінеарними, якщо існує пряма, якою вони паралельні.

Три вектори називаються компланарними, якщо існує площина, якою вони паралельні.

Два вектори називаються рівними, якщо вони колінеарні, однакової довжини і направлені в один бік. Ґрунтуючись на цьому визначенні у вектора можна міняти крапку початку. При цьому три колінеарні вектори лежатимуть в одній площині.

Розкладання вектора по базису

Базисом в просторі називаються три будь-яких не компланарних вектора узятих в певному порядку.

Будь-який вектор можна представити єдиним чином у вигляді лінійної комбінації векторів базису:

де б, в, г називаються координатами вектора в базисі

Вектор базису не можна виразити через інші вектори базису у вигляді лінійної їх комбінації. Говорять, що вектори лінійно незалежні. Додавання будь-якого четвертого вектора до базисних приводить до виконання рівності; говорять, що система векторів, лінійно незалежна.

Окремим випадком базису в просторі є трійкою ортов - векторів одиничної довжини, взаємно перпендикулярних один до одного. Крапка О, з якої виходять орти, є початком декартових координат з осями Ох, Оу, Oz.

Кожен вектор можна спроектувати на осі координат. Розкладання вектора по базису має вигляд:

Тут - проекції вектора на відповідні осі координат.

Якщо вектор задається двома крапками то проекції вектора визначаються різницями координат кінцевої і початкової крапок: (х₂ – х₁), (у₂ – у₁), (z₂ – z₁).

Довжина вектора позначається і обчислюється за формулою:

Множення вектора на число, складання векторів

При множенні вектора на число к виходить вектор При цьому вектори, колінеарні, спів напрями при к > 0 і направлені в різні боки при к < 0. Довжина . Якщо к = 0, виходить нульовий вектор, напрям якого не визначений.

Якщо вектор заданий проекціями на осі координат, то проекції умножаються на число:

При складанні (відніманні) двох векторів складаються (віднімаються) їх проекції:

Якщо вектори задаються в базисі, то формули записують у вигляді

У разі геометричного складання двох векторів точка початку другого вектора переміщається в кінець першого вектора. Замикаючий вектор є сумою (малюнок 1). При складанні декількох векторів будується векторний багатокутник, в якому замикаючий вектор є сумою (малюнок 2).

Приклад виконання завдання

Дано: вектори Показати, що вектори утворюють базис в тривимірному просторі, і знайти координати х₁, х₂, х₃ вектора в цьому базисі.

Векторний твір векторів

Векторним добутком двох векторів називається третій вектор, довжина якого рівна

Вектор перпендикулярний векторам (отже, перпендикулярний площині цих векторів) і направлений так, що трійка векторів – перша, тобто з кінця вектора видно, що поворот вектора до поєднання з вектором по найкоротшому шляху відбувається проти годинникової стрілки.

Векторний добуток рівний нульовому вектору, якщо один з векторів нульовий або вектори колінеарні.

Векторний твір обчислюється за формулою:

З формули виходить, що модуль векторного твору чисельно рівний площі паралелограма, побудованого на векторах, як на сторонах. Площа трикутника, побудованого на цих векторах, рівна половині площі паралелограма. На цьому геометричному факті засновано завдання № 4.

Змішаний твір трьох векторів

Якщо два вектори перемножуються по векторному добутку і результат скалярний умножається на третій вектор, то такий твір векторів називається змішаним.

Змішаний добуток рівний нулю, якщо:

а) один з векторів нульової;

б) два вектори колінеарні;

в) три вектори компланарні.

Змішаний добуток обчислюється як визначник, складений з координат векторів:

Геометричний сенс змішаного добутку полягає в тому, що його модуль рівний об'єму паралелепіпеда, побудованого на векторах, як на ребрах.

При цьому, якщо трійка векторів права, то, якщо трійка векторів ліва, то .

Якщо на тих векторах будувати не паралелограм, а трикутну піраміду – тетраедр, то його об'єм обчислюється за формулою:

На властивості (4) змішані добутки і формулі заснована умова компланарності трьох векторів:

Приклади виконування завдань на фізичний та геометричні властивості векторів, векторного та змішаного добутків

Завдання №1.

Рівняння прямої на площині

На площині із заданою декартовою системою координат XOY положення прямої лінії можна задати різними способами. Відповідно існують різні рівняння прямої на площині. Від одного виду рівняння можна перейти до іншого.

1. Загальне рівняння прямої:

Ах + Ву +z = 0

Коефіцієнти А, В одночасно є координатами вектора нормалі до прямій

2. Рівняння прямої з кутовим коефіцієнтом:

у = kx + b

3. Рівняння прямої, що проходить через задану точку (х0, у0) з кутовим коефіцієнтом:

у = у₀+ у(х₀)(х- х₀)

4. Рівняння прямої, що проходить через задану точку (х_0;у₀) перпендикулярно вектору:

А(х – х₀₎ +В(у-у₀)=0

5. Рівняння прямої, що проходить через дві задані точки (х_1, у₁) (х_2, у₂)

6. Рівняння прямої, що проходить через задану точку (х_0,у₀) паралельно

7. Рівняння прямої у відрізках:

Тут а, b - відрізки, відсічені прямою на осях ОХ, ОУ.

Хай задані дві прямі рівняннями

у =k₁x + b₁ або A₁x +B₁у+ C₁ = 0

у =k₂x + b₂ або A₂x + B₂y + C₂ = 0

Умови паралельності прямих:

Умови перпендикулярності прямих:

Відстань від крапки М (х₀, у₀) до прямій Ах + Ву + С = 0 знаходиться по формулі:

Формула кута між двома прямими має вигляд:

Рівняння площини в просторі

У просторі із заданою декартовою системою координат однозначне розташування площини можна задати різними способами, відповідно існують різні рівняння площини в просторі.

1. Рівняння площини, що проходить через три задані точки

Тут x, у, z – поточні координати точки площини.

2. Рівняння площини, що проходить через задану точку М (x₀, y₀, z₀) перпендикулярно заданому вектору

3. Якщо в рівнянні розкрити дужки і позначити вільний член через D, то отримаємо загальне рівняння площини:

Ax + By + Cz + D = 0

Якщо в загальному рівнянні один з коефіцієнтів А, В, С рівний нулю, то площина проходить паралельно відповідній осі. Якщо два коефіцієнти з А, В, С рівні нулю, площина паралельна одній з координатної площини. Наприклад, площина 4x – 5z – 1 = 0 проходить паралельно осі Оу, площина у + 3 = 0 проходить паралельно координатній площині xOz через крапку у = -3 на осі Оу.

Коефіцієнти А, В, С в загальному рівнянні є одночасно компонентами вектора, перпендикулярного площині.

4. Розділивши рівняння на (-D), отримаємо рівняння площини у відрізках:

Тут а, b, с – відрізки, що відсікаються площиною на осях координат. Наприклад, площина

перетинає осі координат в точках х = 2, у = -3, z = 1.

Відстань від точки М0 (х₀, у₀, z₀) до площини Р, заданої рівнянням визначається по формулі:

Дві площини перпендикулярні (паралельні) один одному, якщо перпендикулярні (паралельні) їх вектори нормалі. Тому, якщо дано дві площини

A₁x +B₁y + C₁z + D₁ = 0

A₂x +B₂y + C₂z +D₂ = 0

та умова перпендикулярності площин:

А₁x + В₁y + С₁z = 0 та

A₂x +B₂y + C₂z +D₂ = 0

Умова паралельності площин:

Питання для самоконтролю:

1. Наведіть приклади скалярних та векторних величин.

2. Які вектори називаються колінеарними ?

3. Як найти суму та різницю векторів ?

4. Як найти координати вектора за координатами його початку та кінця?

5. Назвіть правила складання, находження різниці, які надані у координатній формі. Як помножити вектор на скаляр?

6. Запишіть формулу для находження скалярного добутку двох векторів. Перерахуйте основні властивості скалярного добутку двох векторів.

7. Запишіть формули находження скалярного добутку двох векторів, які задані у координатній формі, для обчислення тангенсу кута нахилу

8. Назвіть умови : колінеарності двох векторів; їх перпендикулярності, компланарності трьох векторів.

9. Який вигляд має рівняння прямої в загальному виді ?

10.Назвіть приватні види прямої; на яких властивостях векторів вони отримані ?

11.Назвіть властивості паралельності та перпендикулярності прямих; на прикладі якої формули можна пояснити ці властивості.

12.Як привести пряму задану у загальному виді до прямої у відрізках, наведіть приклади.

13. Запишіть загальне рівняння площини: запишіть рівняння площини, яка проходить через крапку перпендикулярно даному вектору; який вигляд має рівняння площини, яка проходить через три крапки; запишіть формулу для визначення відстані від крапки до площини; приведіть загальне рівняння площини до рівняння площини у відрізках.

ЛЕКЦІЯ № 3

ТЕМА: Криві другого порядку. Загальне рівняння кривої другого порядку, основні параметри кривих другого порядку; побудова кривих, приведення до канонічного вигляду.

Питання лекції:

_1.1. Загальне рівняння другого степеня з двома змінними.

2. Криві другого порядку.

3. Основні параметри кривих другого порядку; побудова кривих.

4. Приведення кривих другого порядку до канонічного вигляду.

Еліпс, гіпербола, парабола

Загальне рівняння другого степеня з двома змінними х та у має вигляд:

Ax² + 2Bxy+Cy² + Dx + Ey + F=0,

де хоча б один із старших коефіцієнтів А, В, С не дорівнює нулеві.

Лінії на площині, рівняння яких у вибраній декартовій системі координат мають вигляд вищевказаного рівняння, називаються кривими другого порядку. Такими кривими є: коло, еліпс, гіпербола і парабола.

Означення. Еліпсом називається геометричне місце точок площини, для кожної із яких сума віддалей до двох заданих точок, що називаються фокусами, є величина стала.

Якщо позначити через F₁ і F₂ точки, що є фокусами еліпса, а через

М — будь-яку точку, що належить еліпсу, то еліпс характеризується тим,

Рис 1

що

|MF₁| + |MF₂| = const.

Введемо Декартові системи координат так, щоб фокуси F₁ ,F₂ були розташовані на осі Ох, симетрично відносно початку координат (рис. 1). І нехай М(х, у) — будь-яка (біжуча) точка, що належить еліпсу. Віддаль |F₁F₂| позначимо через 2с: |F₁F₂| = 2с, а через 2а — сталу, про яку йде мова в означенні, тобто

|MF₁| + |MF₂| =2a

Очевидно, що для існування еліпса повинно бути 2а > 2с, або а>с. Фокуси еліпса матимуть координати F₁(—с, 0), F₂(c, 0). відстані

між двома точками дорівнюють

де b²=a²-c² (3)

яке називається канонічним рівнянням еліпса.

1. Знайдемо розташування кривої відносно координатних осей. Із (3) дістаємо

звідки |x| ≤ aбо x

звідки |y| ≤ b або y

2.Еліпс розташований симетрично відносно координатних осей, тобто, якщо координати точки М₁(х,у) задовольняють рівняння (3), то його задовольняють і координати точок М₂(—х, у), М₃ (—х, —у),

M₄(x, —у). Отже, еліпс має дві осі симетрії, розташовані на координатних осях. Точка перетину осей симетрії є центром симетрії і називається центром еліпса. Для еліпса, зображеного рівнянням (3), центром є початок координат О(0, 0).

1. Знайдемо точки перетину еліпса з координатними осями. Із (3) дістанемо: якщо х = 0, то у =± b, якщо y = 0, то х =± а. Отже, еліпс перетинає вісь Ох в точках А₁(—а, 0), А₂ (а, 0), а вісь Оу в точках В₁(0, —b), B₂(0, b).

Рис 2

Точки А₁, А₂, B₁, В₂ перетину еліпса з його осями симетрії називаються вершинами еліпса (рис. 2). Відрізки А₁А₂ і B₁B розташовані на осях симетрії. Вони називаються осями еліпса. Відрізок А₁А₂, довжина якого 2а — велика вісь, а В₁В₂ — довжина якого 2b — мала вісь (а> b). Відповідно числа а та b називаються великою і малою півосями еліпса. Відрізок

між фокусами F_lF₂, довжина якого 2с, називається фокальною віссю, тобто с — фокальна піввісь. При цьому числа a, b, c пов'язані співвідношенням

а² ⁼ b²+ с², що очевидно проілюстровано на рис. 2 в AOB₂F₂.

Виходячи із попереднього дослідження, можна побудувати криву-еліпс (рис. 2).

Зауважимо, що зокрема, коли а = b, то рівняння (3) набуває вигляду х² + у² = а². Це рівняння кола із радіусом R = а та центром у початку координат.

4. Фокальною хордою еліпса називається хорда, що проходить через фокус перпендикулярно до його великої осі. Довжина фокальної хорди позначається через 2р. Знайдемо число р — фокальну пів хорду. Якщо Н₁Н₂ (рис. 2) фокальна хорда, то точки Н₁ і Н₂ лежать на еліпсі і їх координати задовольняють рівняння (3). Тому для точки Н₂ (с, р) маємо

тобто

Отже, дістаємо

Числа а, b,с,р є параметрами еліпса.

2. Ексцентриситетом еліпса називається число ε, що дорівнює відношенню фокальної півосі до великої півосі еліпса, і

(4)

оскільки с<а.

Величина ексцентриситету характеризує форму еліпса, його витягнутість по відношенню до осей. Перетворимо (4). Маємо

Звідси випливає, що якщо а = b, то ε = 0, і еліпс перетворюється на коло. Якщо b значно менше, ніж а, то число ε близьке до 1 і еліпс витягнутий вздовж осі Ох.

Аналогічно дістаємо, що |MF₁| = а + εх.

Тоді

|MF₁| + |MF₂|=2a.

Отже, рівняння (1) і (3) еквівалентні.

Величини

r₁=а + εх, r₂ = а — εх,

що є віддалями від точки М(х, у) еліпса до відповідно лівого і правого фокусів, називаються фокальними радіусами точки М(х,у).

Гіпербола.

Означення. Гіперболою називається геометричне місце точок, для кожної із яких абсолютна величина різниці віддалей до двох заданих точок, що називаються фокусами, є величина стала.

Позначимо через F₁ і F₂ точки, що є фокусами, а через М— будь-яку точку, що належить гіперболі. Тоді гіпербола характеризується тим, що

||МF₁| — |MF₂||= const.

Введемо Декартові системи координат так само, як і в попередньому пункті (рис. 1), і позначимо віддаль |F₁F₂| через 2с, а через 2а — модуль різниці віддалі від точки М, що належить гіперболі, до фокусів, тобто

|MF₁| — |MF₂| = 2a. (1)

Очевидно, що повинно бути 2с > 2а, або с> а.

де b²=c²-a².

Рівняння (3) називається канонічним рівнянням гіперболи. Еквівалентність рівнянь (2) і (3) доводиться аналогічно тому, як це зроблено для рівняння еліпса. Зауважимо, що (2) рівняння другого степеня, і гіпербола належить до кривих другого порядку.

Рис 1

(4)

Гіпербола у цьому випадку називається рівнобічною.

3.Назвемо асимптотами* гіперболи прямі

Встановимо взаємне розташування гіперболи та її асимптот. Для цього у вибраній системі координат нарисуємо прямокутник, сторони якого паралельні координатним осям і проходять через вершини гіперболи (рис. 1).

Прямі і

очевидно, проходять через початок координат і співпадають з діагоналями прямокутника.

Для рівнобічної гіперболи (4) а =b і асимптотами будуть прямі у = ±х.

Ексцентриситетом гіперболи називається число ε, що дорівнює відношенню фокальної півосі до дійсної півосі гіперболи, тобто

>1 (5)

оскільки с > а. Ексцентриситет характеризує форму гіперболи.

Рис 2

Перетворимо :

Звідки випливає, що якщо b = а, то гіпербола — рівнобічна. Якщо b<а, то < 1і ε < , причому, чим менше , тим ближче ε до 1, і гілки гіперболи

стиснуті до осі Ох. Якщо ж b>а, то>1іε> , гілки гіперболи

стиснуті до осі Оу.

7. Рівняння

також визначає гіперболу. При цьому число b — дійсна піввісь, число а — уявна піввісь. Ця гіпербола зображена на рис. 2. Якщо ж у

гіперболах

числа а та b одні і ті ж самі, то гіперболи називаються спряженими.

Парабола

Означення. Параболою називається геометричне місце точок площини, кожна з яких рівновіддалена від даної точки, що називається фокусом, і від даної прямої, що називається директрисою (за умови, що директриса не проходить через фокус).

Позначимо через F точку, що є фокусом, через L — пряму, що називається директрисою. Нехай М— будь-яка точка, що належить параболі, ad — її віддаль від директриси. Тоді, згідно з означенням, повинна використовуватись умова:|MF|=d. (6)

Рис 3

Виберемо систему координат так, щоб вісь Ох проходила через фокус F, перпендикулярно до директриси L, а початок координат поділяв навпіл віддаль між фокусом і директрисою (рис. 3. Позначимо через p(p>0) віддаль між фокусом і директрисою. Тоді рівняння прямої L і точка — фокус параболи.

Нехай М(х,у) — будь-яка точка, що належить параболі. Опустимо із М

перпендикуляр МА на пряму L, так що точка А має координати:

Тоді згідно з означенням

|MF| = |MA|.

Маємо

Із (6) дістанемо

(7)

Рівняння (7) є рівнянням параболи у вибраній системі координат. Зведемо його до більш компактного вигляду

(8)

Рівняння (8) називається канонічним рівнянням параболи.

Рівняння (8) є рівнянням другого степеня і парабола є кривою другого порядку, парабола, що задана рівнянням (8), розташована симетрично осі Ох.

Фокальною хордою параболи називається хорда, що проходить
через фокус F, перпендикулярно до осі симетрії. На рис. 3 — це хорда Н₁Н₂. Довжина фокальної |Н₁Н₂| = 2р. Це очевидно із означення
параболи.

Ексцентриситет параболи за означенням покладають рівним 1:

ε=1.

Рівняння х² = 2ру (р>0)

також визначає параболу, але з віссю симетрії, що співпадає з віссю

Оу (рис. 4). Фокус F має координати а директрисою є пряма

На рис. 4 зображена парабола, рівняння якої y² = —2рх, фокус

директриса На рис. 6 зображена парабола,

рівняння якої х² = —2ру, фокус

, директриса .

Рис 4 Рис 5 Рис 6

Питання для самоконтролю:

1. Перелічити основні криві другого порядку.

2. Назвати основні параметри, та особливості побудови кривих другого порядку.

ЛЕКЦІЯ № 4

ТЕМА: Постійні та змінні величини. Функція, способи завдання функції. Основні елементарні функції.

Питання лекції:

1. Поняття функції. (повторення)

2. Способи завдання функції.

3. Основні елементарні функції, властивості функцій.

4. Приклади використання функцій в економіці.

Функція

Постійні величини: наприклад, відношення довжини кола до його діаметру є величиною постійною і дорівнює π.

Змінною величиною називають ту величину, яка може приймати різні числові значення. Наприклад, при рівномірному русі S=v·t, де шлях S і час t- змінні величини, а v – параметр.

Повторення (з курсу математики):

- означення функції (у=f(х) );

- поняття аргументу та функції;

- область визначення (область значення) функції;

- графік функції.

Основні способи завдання функції: табличний, графічний, аналітичний.

Основні властивості функції: парна (непарна); зростаюча (що убуває); монотонна; обмежена (необмежена); оборотна (необоротна); складна функція; періодична.

Основні елементарні функції:

а) статечна функція у=;

б) показова функція у=, а0, а;

в) логарифмічна функція у=, а0, а, х;

г) тригонометричні функції: у=, у=, у=, у=;

д) оборотні тригонометричні функції: у= , у=, у=, у=;

Основні перетворення графіків функцій:

а) здвиг (паралельний переніс) по осі ОХ та ОУ;

б) стиснення (розтягування) по осі ОХ та ОУ;

в) симетрія.

Робота з табличним матеріалом:

Питання для самоконтролю провести з допомогою таблиць (проектора).

ЛЕКЦІЯ № 5

ТЕМА: Границя змінної величини. Важливі границі. Число «е», натуральні логарифми. Розкриття найпростіших невизначеностей.

Питання лекції:

1. Межі, властивості меж .

2. Властивості нескінченно малих .

3. Еквівалентні нескінченно малі.

4.Приклад виконання завдання на межі та їхні властивості.

5. Безперервність функції .

6. Приклад виконання завдання на безперервність функції .

Межі, властивості меж

Число а називається межею послідовності х₁, х₂ ., х_n ., якщо для всякого скільки завгодно малого позитивного числа е знайдеться таке позитивне число N, що |х_n - а| <ε при n > N. В цьому випадку пишуть

(Читається: межа послідовності рівна а при п прагнучому до нескінченності).

Число b називається межею функції f(x) при х > а, якщо для будь-якого скільки завгодно малого е > 0 знайдеться таке д>0, що |f(х) - b| < е при 0 < |х - а| < д. Це записується так:

Аналогічно

Умовно записують

Аналогічно, якщо при

Умовно записують, якщо при, де М – довільне велике позитивне число.

В цьому випадку функція f(x) називається нескінченно великою при х > а.

Функція а(х) називається нескінченно малою при х>а.

Нескінченно великі функції А(х) і нескінченно малі а(х) зв'язані між собою рівністю

або

Якщо х >а і при цьому х<а, то пишуть х>а – 0. Якщо х>а і при цьому х>а, то пишуть х>а+0. В цьому випадку межа називається лівобічною, межа називається правосторонньою. Для існування межі функції при х>а необхідно і достатньо щоб b₁=b₂.

Практичне обчислення меж засноване на наступних їх властивостях:

Використовують також межі (перша чудова межа)

(друга чудова межа).

Властивості нескінченно малих

Еквівалентні нескінченно малі

Нескінченно малі функції володіють наступними властивостями:

1. Сума алгебри нескінченно малих нескінченне мала.

2. Добуток нескінченний малою на постійну, нескінченно малу або обмежену функцію нескінченна мала функція.

3. Якщо а(х) – нескінченно мала, то 1/а(х) – нескінченно велика функція.

Дві нескінченно малих а(х) і в(х) називаються еквівалентними, якщо межа їх відношення рівна одиниці:

а(х) називається нескінченно малою вищого порядку трохи в порівнянні з в(х), при цьому в(х) – нескінченно мала нижчого порядку трохи в порівнянні з а(х).

Якщо відношення два нескінченно малих має межу, то ця межа не зміниться при заміні нескінченно малих їм еквівалентними.

Запис бі ~ у означає, що б і в – еквівалентні нескінченно малі.

При обчисленні меж використовують еквівалентність наступних нескінченно малих:

Якщо х> 0, то:

Крім того, сума нескінченно малих еквівалентна нескінченно малою нижчого порядку трохи, що входить в суму. Так, при х > 0

X³ + 5х² + 8х ~8x

Приклад виконання завдання

1. Щоб розкрити невизначеність вигляду _/_ потрібно розділити чисельник і знаменник на найвищий ступінь зміною, що входить у вираз

2. У завданнях цього пункту має місце невизначеність вигляду 0/0, яка розкривається перетворенням виразу по тригонометричних формулах і застосуванням першої чудової межі (3.3)

3. Щоб розкрити невизначеність вигляду _/_ потрібно розділити чисельник і знаменник на найвищий ступінь зміною, що входить у вираз

4. У завданнях цього пункту має місце невизначеність вигляду 0/0, яка розкривається перетворенням виразу по тригонометричних формулах і застосуванням першої чудової межі (3.3)

При перетворенні враховуємо, що 3х>0, якщо х>0

5. Невизначеність 0/0 розкривається шляхом заміни нескінченно малих складного вигляду ним еквівалентними нескінченно малими простого вигляду.

тут використана еквівалентність

Безперервність функції

Функція у=f(x) називається безперервною в точці х=0, якщо: 1) функція визначена в цій крапці і її околиці; 2) існують односторонні межі при х>а, які рівні між собою; 3) межі рівні значенню функції в цій крапці, тобто

Функція безперервна на відрізку [а, b], якщо вона безперервна в кожній точці інтервалу (а, b), і якщо

Якщо не виконується одна з умов безперервності функції в крапці, то ця крапка є точкою розриву. Залежно від того, які значення приймають односторонні межі в точці розриву, розрізняють точки усуненого розриву (f(a-0)= f(a+0)); точки стрибка, коли кінцеві односторонні межі не рівні між собою; точки розриву 2-го роду, коли односторонні межі не існують або рівна нескінченність.

Приклад виконання завдання на безперервність функції

Задана функція . Знайти точку розриву функції і досліджувати її характер.

РІШЕННЯ. Задана функція визначена при всіх значеннях аргументу, окрім х=3. Тому х=3 – точка розриву функції. Визначаємо односторонні межі в точці розриву.

Хай х>3 зліва, тобто виконується нерівність х<3. Тоді різниця х-3<0 – негативна нескінченно мала величина. Вираз в цьому випадку – нескінченно велика негативна величина. Лівобічна межа:

Хай тепер х>3 справа, тобто виконується нерівність х>3. Тоді різниця х-3>0 – позитивна нескінченно мала величина. Вираз в цьому випадку – нескінченно велика позитивна величина. Правостороння межа

Оскільки одна з односторонніх меж рівна нескінченності, точка х=3 – точка розриву другого роду.

Приклад 1. Обчислити при постійному а.

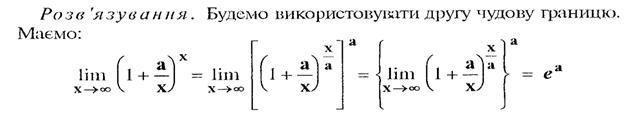
сканирование002

Питання для самоперевірки:

1. Сформулюйте визначення межі числової послідовності.

2. Сформулюйте визначення межі функції.

3. Яка функція називається нескінченно великою? нескінченно малою?

4. Назвіть властивості нескінченно малих функцій.

5. Запишіть формули першої та другої чудових меж.

6. Яка функція називається неперервною у крапці? На інтервалі?

7. Яка крапка називається крапкою розриву першого роду? Другого роду?

8. Назвіть основні властивості неперервних на відрізку функцій.

ЛЕКЦІЯ № 6

Тема: Приріст аргументу та приріст функції. Поняття похідної функції, її геометричний, фізичний та хімічний зміст. Основні правила диференціювання та таблиця похідних. Диференціал функції та його застосування.

Питання лекції:

1. Поняття функції, її графіка; приросту аргументу та функції. (повторення матеріалу зі шкільного курсу математики по малюнку).

4. Приклади використання функцій в економіці.

5. Границя функції. Основні теореми про границі.

6. Неперервність функції; властивості неперервної функції.

7. Поняття похідної та її геометричного, фізичного та хімічного сенсу (повторення ).

8. Правила диференціювання і таблиця похідних основних функцій.

9. Приклад виконання завдання на правила диференціювання і таблицю похідних.

9. Похідні вищих порядків. Приклади находження похідних вищих порядків.

10. Диференціал функції, його властивості і застосування.

Правила диференціювання і таблиця похідних основних функцій

Правила диференціювання і таблиця похідних елементарних функцій розроблена на основі визначення похідної, прийомів і правил обчислення меж. Так, якщо у=С (с = const), то для будь-якого ∆х приріст функції ∆у=0, отже

У цьому полягає перше правило диференціювання. Решту правил вкажемо без доказу.

Правила диференціювання функцій

1. Похідна постійної величини рівна нулю С′=0.

2. Похідна аргументу рівна одиниці. Так, якщо х – аргумент, то х′=1

3. Похідна суми алгебри функцій рівна алгебраїчній сумі (U(x)+V(x)) = U′(x)+ V′(x)

4. Похідна добутку двох функцій (U∙V)′ = U′∙V + U∙V′

5. Постійний множник виноситься за знак похідної (C∙ f(x))′ = C∙(f(x))′.

6. Похідна приватного двох функцій

7. Похідна складної функції. Хай у=f(z), z=q(x). Безліч всіх х, при яких значення z входять в область визначення функції f(z) є областю визначення складної функції у = f(q(x)).

При цьому q(x) називається внутрішньою функцією, функція f називається зовнішньою функцією.

Якщо функція q(x) має похідну в точці х, а функція f має похідну в точці z= q(x), то складна функція у має похідну, рівну твору похідної від зовнішньої функції на похідну від внутрішньої функції

Y׳(х) = f׳(z)·z׳(x).

Таблиця похідних основних функцій:

Приклад. Тут корінь – зовнішня, а синус – внутрішня функції. Якщо позначити

Приклад.

а)

б)

Приклад виконання завдання

на правила диференціювання і таблицю похідних.

У завданні потрібно знайти похідну для різних функцій. У пунктах а), у), з), д), е) використовуються приведені вище за правило диференціювання і таблиця похідних.

У пункті а) задана функція вдає із себе суму алгебри функцій, помножених на постійні величини. Для визначення похідної використовуються правила диференціювання № 1, 3, 5 і таблиця похідних основних функцій.

Приклад.

У пункті в) функція у – добуток двох функцій. Для визначення похідної використовується правило диференціювання № 4.

Приклад.

У пункті з) функція у – участь двох функцій. Для визначення похідної використовується правило № 6.

Приклад.

У пункті д) задана складна функція, похідна визначається за правилом № 7.

Приклад.

. Зовнішньою функцією є корінь квадратний (окремий випадок статечної функції), внутрішня функція – арксинус, яка є зовнішньою для внутрішньої функції – квадратного тричлена.

У пункті с) задана складно-показова функція. Для знаходження її похідної застосовується попереднє логарифмування функції.

Приклад.

Логарифмуємо ліву і праву частину по підставі е:

Тепер диференціюємо, враховуючи, що lny – складна функція, оскільки у=у(х)

Приклад виконання завдання

на находження похідних вищих порядків.

У завданні необхідно знайти першу і другу похідні функції.

Другою похідною називають похідну від похідній і позначають у^''(х).

При повторному диференціюванні звичайних функцій виду у=f(x) справедливі всі правила і таблиця похідних.

а) Знайти у'(х), у''(х), якщо у = х² sin2x.

Рішення. у' = (х²)' sin2x + x²(sin2x)',

y' = 2x sin2x + 2х² sin2x.

y'' = (2xsin2x)' + (2x² cos2x)_ = 2sin2x + 8xcos2x – 4x2 sin2x.

б) Тут функція задана параметрично, тобто незалежна змінна і функція у задані через параметр t:

Похідна у'(х) від функції по змінною х обчислюється за формулою:

де (у(t))^' – похідна від у(t) по параметру t (x(t))'_t – похідна від х(t) по параметру t.

Похідна другого порядку у''(х) від функції по змінною х обчислюється за формулою:

використовуючи вказані формули, знайдемо у'(х), у''(х) для функції

Диференціюємо по t змінні х і у:

Для визначення другої похідної першу похідну у''(х) диференціюємо по t:

Розділимо отриманий вираз на х'(t) і знайдемо у''(х):

Диференціал функції, його властивості і застосування

Розглянемо функцію у = f(x). За визначенням похідної

Звідки де а – нескінченно мала при х>0, тобто а>0. Помножимо останню рівність на х.

У першій частині рівності (3.14) доданок αΔх – нескінченно мала нижчого порядку трохи в порівнянні з доданком у'Δх, воно вважається головною частиною приросту функції у і називається диференціалом функції, що позначається так:

(3.15)

Властивості диференціала

1. Диференціал аргументу рівний його приросту.

2. Диференціал функції еквівалентний приросту функції при х>0, тобто dy~∆y.

3. Диференціал функції обчислюється за формулою (3.15), де dх=∆х.

4. Властивість інваріатності форми диференціала полягає в тому, що диференціал складної функції має той же вигляд, який він мав би в тому випадку, якщо б проміжний аргумент і був незалежною змінною:

5. Оскільки завдання знаходження диференціала рівносильне знаходженню похідної, то правила диференціювання функцій зберігають свою силу і для диференціала, а саме:

Диференціал функції знаходить застосування в наближених обчисленнях, заснованих на формулі:

Формула виходить з еквівалентності ∆у ~dy

Якщо відоме значення функції при х = х0, то використовуючи (3.16) легко знайти значення функції при х = х₀ + х.

Питання для самоперевірки:

1. Дайте поняття приросту аргументу та функції.

2. Назвіть основні елементарні функції, властивості функцій.

3. Наведіть приклади використання функцій в економіці.

5. Дайте поняття похідної та її геометричного, фізичного та хімічного сенсу похідної.

6. Дайте поняття похідної вищих порядків.

7. Дайте поняття диференціалу та його використання у наближених численнях.

ЛЕКЦІЯ № 7

Тема: Застосування похідної для дослідження функції. Екстремум функції. Необхідна і достатня умова існування екстремуму функції. Загальні дослідження функції та побудова графіка функції.

Питання лекції:

1. Теореми Роллю, Лагранжа та їхній геометричний змісти.

2. Поняття зростаючої та убиваючої функцій.

3. Необхідний та достатній признаки зростаючої та убиваючої функцій.

4. Критичні крапки. Екстремуми функції (необхідні та достатні умови існування екстремуму функції).

5. Інтервали опуклості та угнутості графіків функцій.

6. Необхідна та достатня умови існування точок перетину графіків функцій.

7. Визначення асимптот кривої, формули для находження асимптот кривої. Загальний план дослідження функцій і побудова графіків.

8. Випадки використання правила Лопіталя при обчисленні меж. Приклад виконання завдання .

9. Випадки використання похідної для знаходження найбільшого та найменшого значень.

Застосування 1-ої і 2-ої похідної для дослідження функції

Розглянемо графік функції у = f(x) на малюнку. Дослідження функції включає крім інших питань визначення інтервалів зростання і убування функції, а також пошук точок максимуму і мінімуму (точок екстремуму). Геометричний сенс похідної дозволяє визначити ці особливості функції. Малюнок 11 – Графік функції у = f(x)

Максимум функції

δ х₁ х₂ Х

Мінімум f(x)

1. Функція є такою, що зростає на тих інтервалах, де її похідна позитивна. На малюнку 11 це інтервали (-; х₁) (х₂, ). На вказаних інтервалах кут нахилу дотичної до графіка функції гострий, отже tgδ = у > 0.

2. Функція убуває на інтервалах, де її похідна негативна, оскільки там tgδ = у < 0. На малюнку інтервал убування функції (х₁, х₂).

Необхідною умовою існування екстремуму функції є рівність нулю її похідної або відсутність похідної в деяких крапках, які називаються критичними. Щоб в цих крапках існував екстремум функції повинна виконуватися достатня умова екстремуму: якщо під час переходу через критичну крапку знак похідної міняється з «+» на «-», то в даній крапці є максимум функції; якщо похідна міняє знак з «-» на «+», то в такій критичній крапці функція має мінімум. Для існування екстремуму, крім того, функція повинна бути безперервною в критичній крапці.

На малюнку 11 в крапці х₁ функція має максимум, в точці х₂ – мінімум. Дотична до графіка функції в цих крапках паралельна осі аргументу. Якщо коштує завдання визначення найбільшого і найменшого значення функції на відрізку, то її потрібно вирішувати в наступній послідовності:

1. Визначити критичні крапки.

2. Обчислити значення функції в критичних крапках і на кінцях відрізання.

3. Вибрати із знайдених значень функції найбільше і найменше.

Друга похідна у´´(х) застосовується для визначення інтервалів опуклості і угнутості графіка функції. Принцип визначення таких інтервалів показаний на малюнку 12. Крапка, лежача на межі між опуклістю і угнутістю, називається точкою перегину.

графік увігнутий

точка перегину

графік опуклий

Загальний план дослідження функцій і побудова графіків

Наочне уявлення про функцію дає її графік. Побудова графіка служить завершальним етапом дослідження функції. При дослідженні функції визначаються:

1. Природна область існування функції, точки розриву і їх характер, наявність вертикальних асимптот графіка.

2. Симетрія графіка функції (парність або непарність функції), точки перетину графіка з осями координат.

3. Похилі і горизонтальні асимптоти графіка.

4. Інтервали зростання і убування функції, екстремуми.

5. Інтервали опуклості і угнутості графіка, точки перегину.

6. Складання звідної таблиці результатів дослідження.

7. Побудова графіка.

Приклад виконання завдання

Досліджувати методами диференціального числення функцію

і, використовуючи результати дослідження, побудувати її графік.

РІШЕННЯ: 1. Область існування – вся числова вісь за винятком точок х = -2, х = 2. Це точки розриву. Визначуваний характер точок розриву.

Оскільки гілки кривої прагнуть до нескінченності при х>-2, і при х> 2, то в цих крапках – розрив другого роду, є вертикальні асимптоти з рівняннями

х=- 2, х = 2.

Визначаємо точки перетину графіком осей координат. Якщо х = 0=> у = 0. Якщо у = 0 =>х = 0. Є одна крапка – початок координат.

2. Оскільки, то функція є непарною. Графік функції симетричний відносно початку координат.

Примітка: Якщо f(-х)= f(x), то функція парна, графік симетричний щодо вертикальної осі; якщо f(-х)_ -f(x) і f(-х)= f(x), то графік не володіє симетрією щодо осі Оу і початку координат, функція – загального вигляду.

Якщо існує кінцева межа

то графік має горизонтальну асимптоту з рівнянням у = b. У нашому випадку горизонтальної асимптоти немає.

Якщо існують дві кінцеві межі, то графік має похилу асимптоту з рівнянням у = kx+ b .

Для нашого прикладу

Таким чином існує асимптота похилої в рівнянні у=х

Визначаємо першу похідну

Критичні точки х=-23, х=0, х=23 (похідна рівна нулю) і точки х=-2, х=2 (похідна не існує).

Знаки першої похідної визначаємо методом інтервалів

у׳ + - - - - +

-2√3 -2 0 2 2√3

Друга похідна у´´=

Друга похідна рівна нулю при х=0 і не існує при х=-2, х=2

Знаки другої похідної визначаємо методом інтервалів

у^” - + - +

-2 0 2

Результати дослідження узагальнюємо за допомогою таблиці

Таблиця – Результати дослідження функції

Значення аргументу х	Значення функції у	Знак у	Знак у^”	Виведення функції
-<х<-23	-	+	-	Зростає, опуклість
х=-23	-23	0	-	Максимум функції
-23<х<-2	-	-	-	Убуває, опуклість
х=-2	Не сущий.	Не сущий.	Не сущий.	Вертикальна асимптота
-2<х<0	+	-	+	Убуває, угнутість
х=0	0	0	0	Точка перегину
0<х<2	-	-	-	Убуває, опуклість
х=2	Не сущий.	Не сущий.	Не сущий.	Вертикальна асимптота
2<х<23	+	-	+	Убуває, угнутість
х=23	23	0	+	Мінімум функції
х>23	+	+	+	Зростає, угнутість

На підставі виводів таблиці результатів дослідження будуємо графік функції

Малюнок 13. Графік функції до завдання 13

Питання для самоперевірки:

1.Сформулюйте теореми Роллю, Лагранжа та поясніть геометричний сенс.

2. Сформулюйте умови зростаючої та убиваючої функцій,

необхідний та достатній признаки зростаючої та убиваючої функцій.

4. Які крапки називають критичними та які з них є екстремумами?

5. Як знайти інтервали опуклості та угнутості кривої?

6. Запишіть формули, за якими знаходять асимптоти кривої.

7. Назвіть схему дослідження функцій та побудови графіка кривої.

8. Наведіть приклади застосування правила Лопіталя.

9. Алгоритм використання похідної для знаходження найбільшого та найменшого значень.

ЛЕКЦІЯ № 8

Тема: Первісна функція та невизначений інтеграл. Основні властивості невизначеного інтегралу, таблиця інтегралів. Невизначений інтеграл. Табличне інтегрування.

Питання лекції:

1. Первісна. Невизначений інтеграл.

2. Таблиця інтегралів і таблична інтеграція.

3. Безпосереднє інтегрування.

4. Вказівки до виконання завдань на безпосереднє інтегрування.

5. Суттєвість інтегрування методом підстановки, інтеграції по частинах.

Первісна. Невизначений інтеграл

Функція F(x) називається первісною для функції f(x) в інтервалі (а,b), якщо для всіх х € (а, b) виконується рівність

F׳(х) = f(х).

Визначення первісною для заданої функції називається інтеграцією цієї функції. Інтеграція – дія зворотна диференціюванню і практично складніше.

Первісна для заданої функції не є єдиною. Так, F(x)= cosx – первісна для функції f(x)= -sinx, оскільки (cos x)` = -sinx. Але і (cos x + 5)` = sinx. Якщо відома одна первісна F(x), то будь-яка інша має вид F(x)+ C, де С – довільна постійна.

Якщо функція F(x) є первісною для f(x), то вираз F(x)+ C називається невизначеним інтегралом і позначається

Тут f(x) – підінтегральна функція, х – змінна інтеграції, dx – диференціал змінної інтеграції

З визначень і правил диференціювання витікають властивості невизначеного інтеграла:

1. Похідна від невизначеного інтеграла рівна підіинтегральної функції.

2. Диференціал від невизначеного інтеграла рівний підіинтегральному виразу.

3. Невизначений інтеграл від диференціала деякої функції рівний цій функції плюс довільна постійна.

4. Невизначений інтеграл від суми алгебри функцій рівний сумі алгебри інтегралів цих функцій.

5. Постійний множник можна винести за знак інтеграла.

Таблиця інтегралів і таблична інтеграція

Значення інтегралів від основних елементарних функцій отримані на основі формул диференціювання.

Примітка: змінна інтеграції U в таблиці інтегралів – довільна функція, що диференціюється.

Метод табличної (безпосередньої) інтеграції полягає в тому, що за допомогою еквівалентних перетворень функції і на підставі властивостей невизначеного інтеграла задані інтеграли перетворяться до табличних. Це дає можливість безпосередньо записати первісну.

Приклад

При інтеграції були використані властивості № 3,4, 5 невизначеного інтеграла і табличні інтеграли № 1, 2, 5.

При безпосередній інтеграції часто застосовується прийом підведення функції під знак диференціала, заснований на властивості № 6. З урахуванням того, що диференціал функції визначається по формулі

df(x)= f׳(x) dx

У підинтегральному виразі потрібно відшукати функцію, яку приймаємо за f׳(x) і підводимо під знак диференціала .

Інтеграція підстановкою

Метод полягає в перетворенні аргументу підінтегральної функції по деякій формулі, розрахованій на те, щоб інтеграл з новою змінною виявився простішим для обчислення. Після обчислення інтеграла з новою змінною потрібно повернутися до первинної змінної інтеграції.

Приклад 2 Знайти інтеграл

Застосуємо підстановку x = 2sint, тоді dx = 2costdt

Інтеграл з новою змінною виявляється табличним:

Застосування різних підстановок розглянуте у підручнику 2 стор.

Інтеграція по частинах. Вказівки до виконання завдання.

Формула методу інтеграції по частинах має вигляд:

Тут U, V – дві функції аргументу х, що диференціюються.

Метод інтеграції по частинах полягає в наступному.

Підінтегральну функцію початкового інтеграла розглядаємо як добуток функції U і диференціала деякої функції dV. За диференціал dV ми повинні вибрати вираз, для якого зможемо знайти первісну.

Після цього застосовуємо формулу (3.3). Застосовувати формулу має сенс у тому випадку, коли інтеграл виявиться простішим початкового або подібний до нього. Для отримання остаточного результату іноді потрібно застосувати метод послідовно кілька разів.

Приклад 1

Покладемо U = x, dV = cosxdx. Тоді dU = dx

Застосовуємо формулу (3.3)

Методом інтеграції по частинах обчислюються інтеграли наступних типів (список інтегралів можна розширити):

Примітка: У інтегралах 1,2,3 функцію U слід приймати хⁿ. У інтегралах 4,5 байдуже, що приймати за U, але формула застосовується двічі. У інтегралах 6-10 слід прийняти .

Інтеграли в завданні 6 обчислюються методом інтеграції по частинах. Використовуйте формулу (3.3) і рекомендації до вибору функції U і dV. У варіанті 6 застосуєте спочатку формулу cos2x = 0.5(1+cos2x),у варіанті 9 використовуйте формулу Якщо при обчисленні отриманий по формулі (3.3) інтеграл складніше початкового, зміните вибір функції U і dV.

Таблиця інтегралів